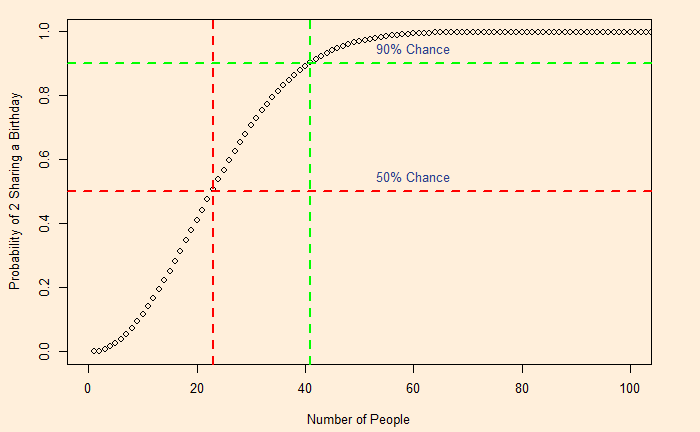
The birthday problem. What is the minimum number of people required to be in a room to have a 90% chance that at least two individuals share a birthday? The answer is about 41 people. You may have guessed more than 41; the puzzle has led to people overestimating the number.
We will see the calculations but a few basic probability concepts first.
Two definitions
Independent Events. Two events are independent if one does not affect the other. Two flips of a coin: the outcome from the second is independent of the first outcome.
Mutually Exclusive Events. When one happens, the other can not occur. Examples are day and night, winning and losing a game, or turning left and right in one.
1. The law of multiplication (AND Rule)
For independent events, the joint probability of occurrence of one and the second is obtained by multiplying their individual probabilities.
P (A and B) = P(A) x P(B)
Flip a coin twice: the chance of getting two heads in succession is equal to the chance of getting the first head x chance of getting the second head. The probability of each is 1 in 2. So the overall probability P (head and head) = (1/2) x (1/2) = 0.25 (25% chance).

Note that this AND rule is a special case of a general Conjunction Rule that says
P(A and B) = P(A) x P(B given A)
[if A and B are independent, P(B given A) = P(B)]
An example: the probability of drawing two Aces from a deck of cards (no replacement). It is given by multiplying the probability of getting the first ace (4/52), and the second given the first is an ace (3/51) = 12/(52 x 51) = 1/221.
2. The Law of addition (OR Rule)
The probability of getting A or B is equal to the probability of getting A plus the probability of getting B minus the probability of A and B.
P (A or B) = P(A) + P(B) – P (A and B)
The equation simplifies when the events are mutually exclusive, or P (A and B) = 0 (both can not happen at once)
P (A or B) = P(A) + P(B).
I throw a 6-sided dice, and the chance of getting 1 or 3 is = (1/6)+(1/6) = 2/6.

3. The law of subtraction
The probability of something to occur is equal to 1 minus the probability that it does not occur.
P(A) = 1 – P(A’)
The Birthday Problem
Let’s build the solution from the smallest group. What is the probability of two people sharing a birthday in a group of 2? To answer this, we first go to the inverse problem – the chances of two people not sharing a birthday – and subtract that from 1 (using the subtraction rule because you can not have unique and shared birthdays at once).
- The chance of one person having a unique birthday = 1
- The chances that the second person does not share the previous birthday = 364 available days in 365 = (364/365)
Using the AND rule, we calculate the probability of the two having unique birthdays. It is because the second person’s birthday is not affected by the birth of the first person (independent events).
So, it is 1 x (364/365).
If we extend this logic for a group of 3, the probability becomes 1 x (364/365) x (363/365). So, for 20 people, it becomes
1 x (364/365) x (363/365) x … x (346/365) = 0.58.
Therefore, the chance of at least one shared birthday in a group of 20 is equal to (1 – nobody shares) = (1 – 0.58) = 0.42 (42%)
For a group of 41, it is [1 – 1 x (364/365) x (363/365) x … x (325/365)] = [1 – 0.10] = 0.90 (90%)
So the minimum number of people for a 90% chance to share a birthday is 41