The Small Sample Fallacy

You may remember an older post titled “Life in a Funnel“. It discussed the wired (i.e., extreme) variation of averages (of the rate of certain illnesses, income levels, etc.) arising from groups and places with smaller populations. An often-quoted example is the prevalence of the lowest rates of kidney cancer in the US. These are regions of often rural, sparsely populated, traditionally Republican states. People who come across this data would rationalise this to cleaner air, healthier lifestyles or fresh foods. But when it comes to regions with the highest prevalence of the same disease, they also belong to mostly rural, less populated, Republican!

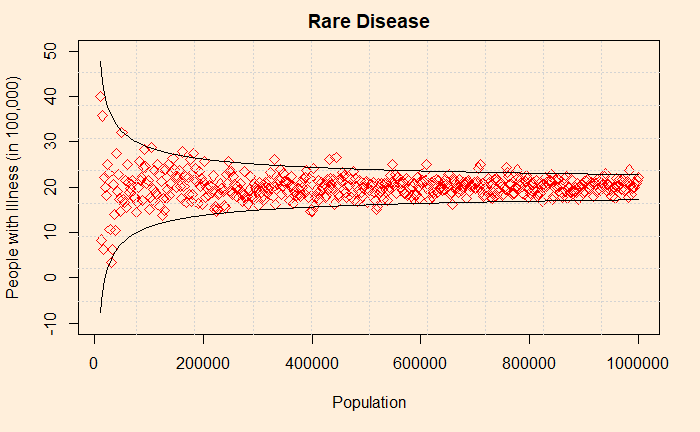
The plot shows the variability of observed averages simulated from precisely the same incident rate. As the sample size decreases, the sample average goes up or down dramatically, creating an illusion that forces the public to believe something real. This is known as the small sample fallacy. It’s a mistake where one attaches a causal explanation to a statistical artefact due to a smaller sample size.

A simple illustration is to imagine a bowl containing several marbles – 50% red and 50% green. If you take only four samples out of it to check the proportion, there is a 12.5% chance of getting either all green or all red. Work out this binomial probability with p = 0.5, n = 4 and x = 4.
P(X=4 red) = ₄C₄ 0.5⁴ 0.5⁰ = 0.0625
P(X=4 green) = ₄C₄ 0.5⁴ 0.5⁰ = 0.0625
P(all red or all green) = 0.0625 + 0.0625 = 0.125 or 12.5%.

There is a 12.5% chance of seeing an extreme sample average from an otherwise perfectly balanced population. In other words, 12 investigators out of 100 will see a distorted value!

Now, increase the samples to 10, the probability of observing all red or all green reduces dramatically to,
P(all red or all green) = ₁₀C₁₀ 0.5¹⁰0.5⁰ + ₁₀C₁₀ 0.5¹⁰0.5⁰
P(all red or all green) = 0.00098 + 0.00098 = 0.00196 or just 0.2%.

Reference

The Small Sample Fallacy: Kevin deLaplante