Amy walks into a raffle house and finds it about to close. They are raffling off an object with a value of $1000. She finds that only 200 tickets have been sold. Knowing they will draw the winner at any time, how many tickets should Amy purchase to maximise the expected value? The cost is $1 per ticket.
The expected payoff = expected value of the lottery – the price you paid.
= value of the object x the probability of winning – the price you paid.
the probability of winning = # ticket you bought / total # tickets sold.
If x is the number of tickets Amy purchased,
The expected payoff = [1000 * x /(200 + x)] – x
So, we need to find the x that maximises the payoff. One way to determine is to plot the expected payoff ([1000 * x /(200 + x)] – x) as a function of the # tickets (x) you purchased and see where it maximises.
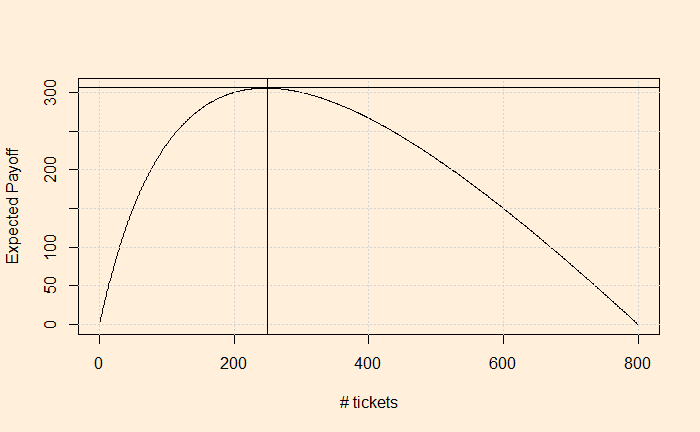
The number of tickets that maximises the expected payoff is somewhere close to 250.
What’s the Best Raffle Strategy?: William Spaniel

