In the previous post, we have seen a variation of the 100 prisoners problem applied to the Monty Hall problem. But what is the 100 prisoners problem?
One hundred prisoners numbered 1 to 100 are given a choice to free themselves if they all find their numbers, written on a piece of paper, randomly kept inside 100 boxes numbered 1 to 100. In other words, the bit carrying number 8 could be inside box 64, #21 inside box 99 etc. The room that keeps the boxes allows only one prisoner at a time, and he can open a maximum of 50 boxes. Even if one fails in his attempt, the whole group loses, and none will walk free. Prisoners can discuss strategies only before the game.
The Strategy
Suppose each player tries opening boxes at random. The probability of a person finding his number from 100 boxes by opening 50 is (50/100) or (1/2). For 100 people to find their numbers, the chances are (1/2) multiplied 100 times or (1/2100), a number close to zero.
Instead, they decide on a strategy; the person first opens the box that carries his number. If he finds his number, fine or else he goes to the box that corresponds to the number inside the first box. It continues until one of the two things happens. He finds his number, or he reaches the maximum of 50 attempts. This strategy can raise the probability of success to a mind-boggling 31%!
To understand this, take the case wherein the prisoner finds his number inside a box. If he continues the strategy, the number he just discovered, which is his number, will lead to the container that carries his number, which is nothing but the first one he opened. Or he always completes a circle of 50 (or lower) boxes if he is successful. Every unsuccessful attempt means the (unfinished) loops are longer than 50.
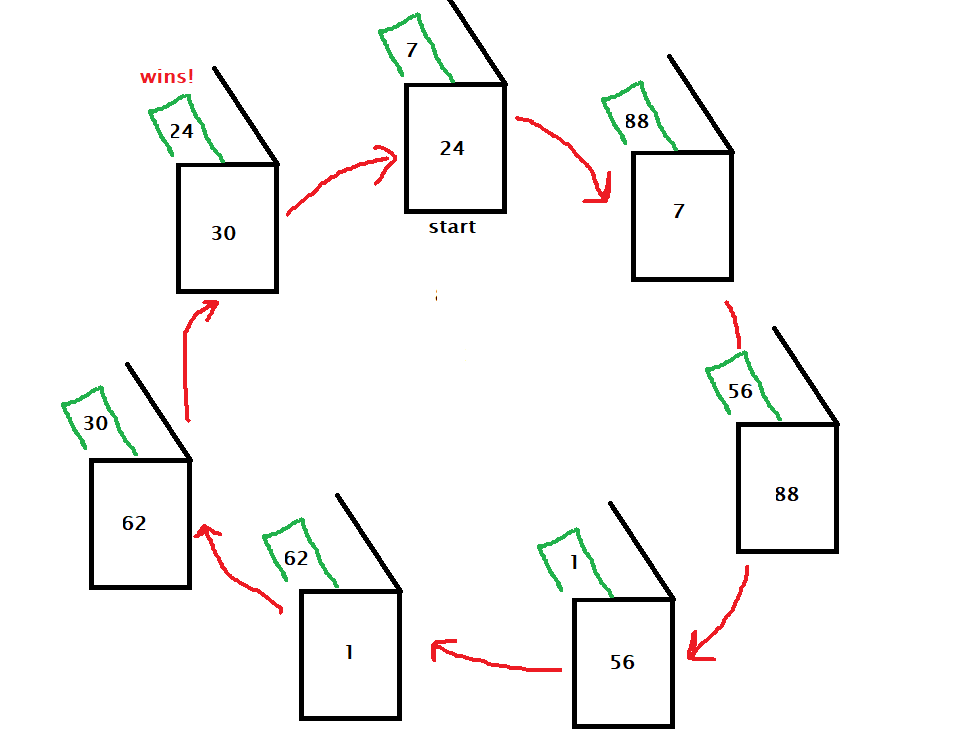
Each prisoner makes one loop
So the problem becomes the collection of such loops. The probability that such a cluster has no loop larger than 50 is 31%.

