We continue from where we stopped last time and develop an R code for survival analysis.
We need to code 1 for people who experienced the event, and the censored ones (who haven’t experienced or left the group) get 0. Note that you can substitute indicator 2 for 1 and 1 for 0. The following are the first ten entries of the data frame.
| group | weeks | Illness |
| Treatment | 6 | 1 |
| Treatment | 6 | 1 |
| Treatment | 6 | 1 |
| Treatment | 6 | 0 |
| Treatment | 7 | 1 |
| Treatment | 9 | 0 |
| Treatment | 10 | 1 |
| Treatment | 10 | 0 |
| Treatment | 11 | 0 |
| Treatment | 13 | 1 |
The survival package
The first thing we want is the ‘survival’ package. After installing the package, type the following commands.
ill_fit <- survfit(Surv(weeks, illness) ~ group, data = ill_data1, type = "kaplan-meier")
summary(ill_fit)
par(bg = "antiquewhite1")
plot(ill_fit, col = c("blue", "red"), xlim = c(0,35), xlab = "Time in weeks", ylab = "Survival Probability")
legend("topright", legend = c("Control", "Drug"), col = c("blue", "red"), lty = c(1,2))And the output is:
Call: survfit(formula = Surv(weeks, illness) ~ group, data = ill_data1,
type = "kaplan-meier")
group=Control
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 21 2 0.9048 0.0641 0.78754 1.000
2 19 2 0.8095 0.0857 0.65785 0.996
3 17 1 0.7619 0.0929 0.59988 0.968
4 16 2 0.6667 0.1029 0.49268 0.902
5 14 2 0.5714 0.1080 0.39455 0.828
8 12 4 0.3810 0.1060 0.22085 0.657
11 8 2 0.2857 0.0986 0.14529 0.562
12 6 2 0.1905 0.0857 0.07887 0.460
15 4 1 0.1429 0.0764 0.05011 0.407
17 3 1 0.0952 0.0641 0.02549 0.356
22 2 1 0.0476 0.0465 0.00703 0.322
23 1 1 0.0000 NaN NA NA
group=Treatment
time n.risk n.event survival std.err lower 95% CI upper 95% CI
6 21 3 0.857 0.0764 0.720 1.000
7 17 1 0.807 0.0869 0.653 0.996
10 15 1 0.753 0.0963 0.586 0.968
13 12 1 0.690 0.1068 0.510 0.935
16 11 1 0.627 0.1141 0.439 0.896
22 7 1 0.538 0.1282 0.337 0.858
23 6 1 0.448 0.1346 0.249 0.807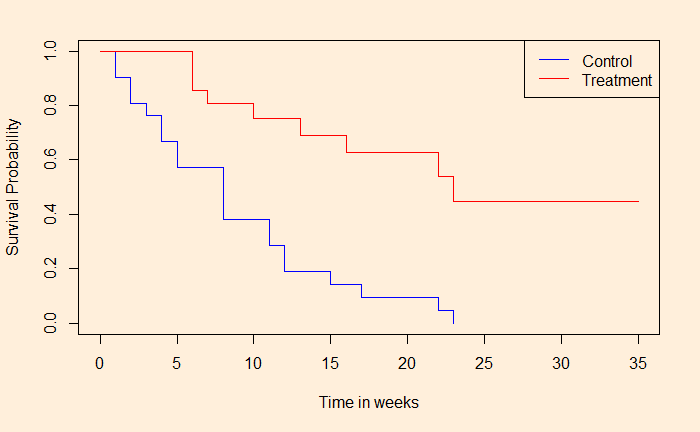
We can see the difference in survival chances for people who had undergone treatment vs those who had not. Is this significant, and if so, how much is the difference? We will see next.

