Based on what we have seen so far, let’s put together three strategies for games we have encountered in the past. But before delving into those, look at Nash’s theorem, which suggests that there must be at least one Nash equilibrium in all finite games. Watch out for those two words: Nash equilibrium and finite games!
A finite game has a fixed number of players, a defined set of rules, and a known end.
Nash equilibrium is the state of a game where the player has made her best decision or has no incentive to change the decision, assuming all other players maintain their current strategy.
The dominant strategy
Remember the prisoner’s dilemma? The prisoner has a clear move irrespective of what the others will do. To put it in the language of the payoff matrix,
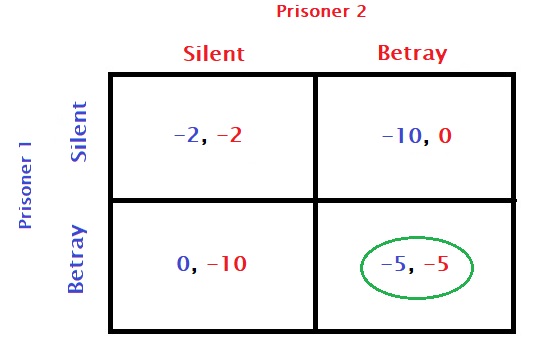
The pure strategy
The stag hunt game;
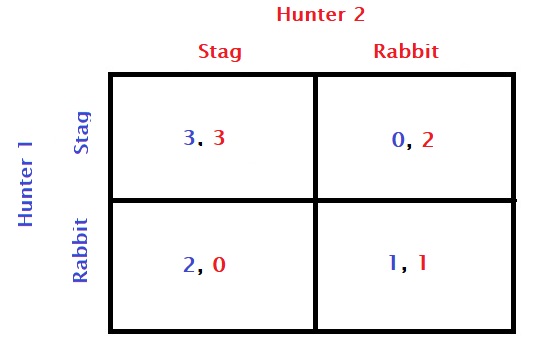
Compare dominant and pure
In the first instance, they may appear the same: one best outcome, one sub-optimal and two places with mixed incentives. But look carefully: in the first game, imagine you are prisoner 1, and think about your reward (the blue number) based on the two possibilities of the other player. If prisoner 2 is silent (first column), then your choice is to betray as 0 > -2 (compare the two blue numbers of the first column). If prisoner 2 chooses to betray (second column), your choice is still to betray as -5 > -10 (compare the two blue numbers of the second column). 100% clarity!
In the second case, repeat the above process. If hunter 2 brings the tool for the stag, the stag becomes your choice (blue 3 > blue 2). If hunter 1 gets the rabbit device, the rabbit is your choice (blue 1 > blue 0).
The mixed strategy
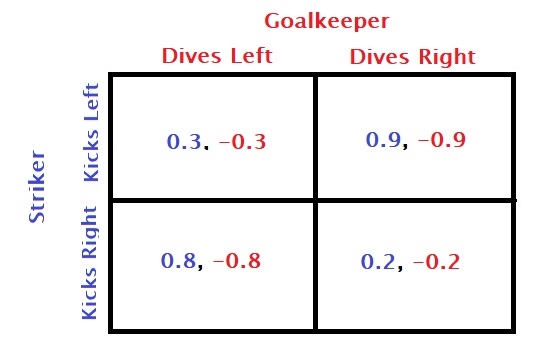
The penalty kick game is an example of a zero-sum game—one person’s win is the other’s loss. There is no pure strategy here; one needs to mix up (randomise) the plan to succeed. In other words, the strategy needs probabilistic estimation.

