Skewness and Kurtosis

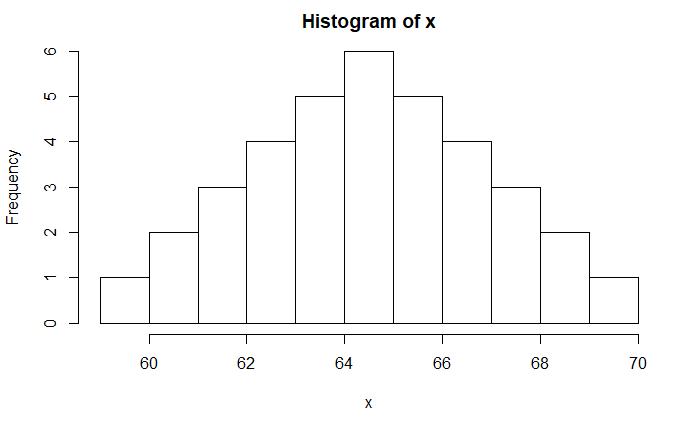
Skewness is the measure of symmetry or the lack of it. A symmetric dataset means data is distributed equally on the left and right of the mean (or median). Following is an example of a symmetric distribution.

Skewness

It is defined as (Pearson’s moment coefficient of skewness)

g_1 = \frac{\sum\limits_{i = 1}^n(X_i - \mu)^3 / n}{\sigma^3} \\ \\ \text{After adjusting the formula for the sample size, }n \\ \\ G_1 = \frac{\sqrt{n(n-1)}}{n-2} g_1 \\ \\ \text{Note that for large } n \text{, } G_1 \text{becomes } g_1

The skewness of the data is close to zero for symmetric distribution, which is the case with the figure above. A positive value for g1 indicates positive skewness or right-tailed, and a negative g1 is for negative skewness or left-tailed.

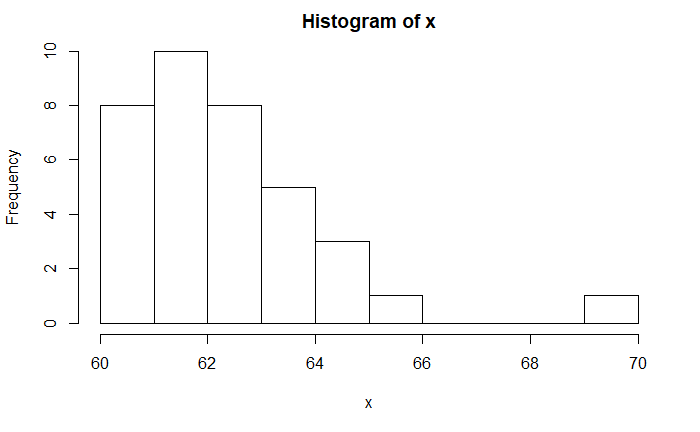
Following is an example of a positively skewed distribution (right-tailed). Its skewness is calculated to be 1.08 using the R function, ‘skewness’ (you must install library ‘moments‘ for that).

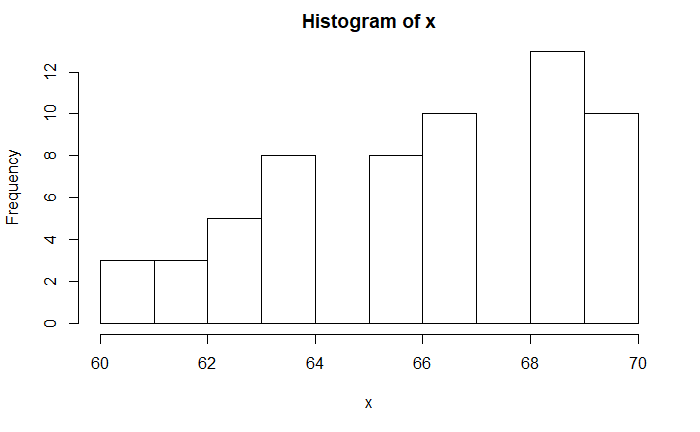
In the same way, the skewness of the following plot is -0.43; it is a negatively skewed distribution (left-tailed).

Kurtosis

Kurtosis is the measure of how heavy or light the tail is.

\\ \text{Kurtosis} = \frac{\sum\limits_{i = 1}^n(X_i - \bar{X})^4 / n}{\sigma^4} \\ \\ \text{Excess kurtosis} = \frac{\sum\limits_{i = 1}^n(X_i - \bar{X})^4 / n}{\sigma^4} - 3\\ \\

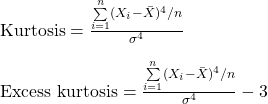
A kurtosis value of 3 indicates standard normal distribution. Excess Kurtosis (Kurtosis – 3) is a deviation from a standard normal distribution.

Finally, the codes used to generate those distributions and their properties. 

library(moments)


x <- c(rep(59.99999, each = 1), rep(61, each = 2), rep(62, each = 3), rep(63, each = 4), rep(64, each = 5), rep(65, each = 6), rep(66, each = 5), rep(67, each = 4), rep(68, each = 3), rep(69, each = 2), rep(70, each = 1))
hist(x, breaks = 10)

skewness(x)
kurtosis(x)

x <- c(rep(60, each = 8), rep(62, each = 10), rep(63, each = 8), rep(64, each = 5), rep(65, each = 3), rep(66, each = 1), rep(70, each = 1))
hist(x, breaks = 10)

skewness(x)
kurtosis(x)

x <- c(rep(60, each = 1), rep(61, each = 2), rep(62, each = 3), rep(63, each = 5), rep(64, each = 8),
rep(66, each = 8), rep(67, each = 10), rep(69, each = 13), rep(70, 10))

hist(x, breaks = 10)
skewness(x)
kurtosis(x)

Related Posts