Shaq Goes to the White House

Shaquille O’Neil, popularly known as Shaq, is a basketball player and four-time NBA champion. He once had a bet with his friend about getting into the White House without prior permission. The wager was 1000 push-ups.

What is the chance of Shaq to be successful?

We can use binomial probability mass function (PMF) to estimate Shaq’s chance.

f(s; n,p) = \binom{n}{s} p^s (1-p)^{n-s}

Where n is the number of trials, s is the number of successes, and p is the probability of success.

Since Shaq was confident to bet, one can imagine that he would have given a higher value of p (say 0.9) for himself, whereas his friend would think lower (say, 0.2). If Shaq has one chance to show up, called a Bernoulli trial, associated probabilities with those two conditions are:

\\ f(1; 1,0.9) = \binom{1}{1} 0.9^1 (1-0.9)^{1-1} = 0.9 \text { and} \\ \\ f(1; 1,0.2) = \binom{1}{1} 0.2^1 (1-0.2)^{1-1} = 0.2

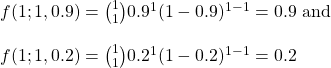
If Shaq makes three attempts, as per his view, the success rates are:

\\ f(s; 3,0.9) = \binom{3}{s} 0.9^s (1-0.9)^{3-s} \\ \\ \text{for s = 0, no success} \\ f(0; 3,0.9) = \binom{3}{0} 0.9^0 (1-0.9)^{3-0} = 0.001 \\ \\ \text{for s = 1, 1 success} \\ f(1; 3,0.9) = \binom{3}{1} 0.9^1 (1-0.9)^{3-1} = 0.027 \\ \\ \text{for s = 2, 2 successes} \\ f(2; 3,0.9) = \binom{3}{2} 0.9^2 (1-0.9)^{3-2} = 0.243 \\ \\ \text{for s = 3, 3 successes} \\ f(3; 3,0.9) = \binom{3}{3} 0.9^3 (1-0.9)^{3-3} = 0.729

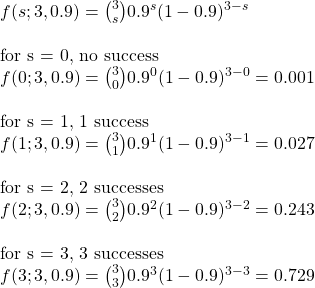
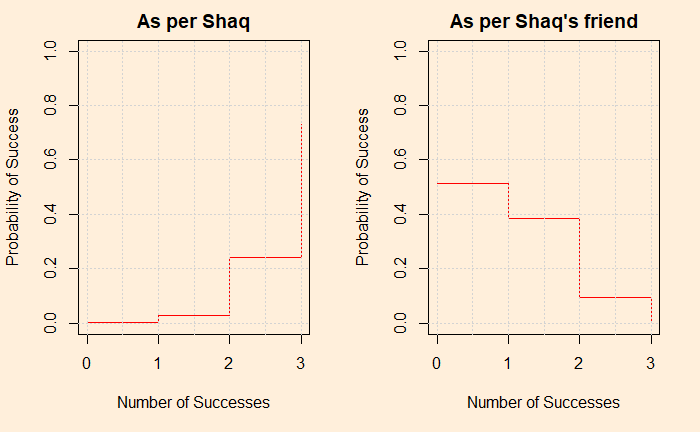
The probability densities for Shaq and his friend, in graphical format, are:

Was Shaq successful?

No, he was not. He tried once but was stopped at the gate by the security! What would have happened had he made another attempt? More about that story and the use of Baysian in the next post.

Shaq Denied Entrance: Washington Post

Related Posts