Schools of Inference

There are two approaches to statistical inference, and we have briefly touched upon those in the past. They are the frequentist approach and the Bayesian approach.

Frequentists count the occurrences and estimate probability as the limiting frequency. They take random samples from the population and find fixed parameters (theta) of the distribution. Their objective is to create the confidence interval and capture the parameter inside it.

$\\ C = \left[ \bar{X_n} - \frac{1.96}{\sqrt{n}}, \bar{X_n} + \frac{1.96}{\sqrt{n}} \right] \\ \\ \mathbb{P}_{\theta} (\theta \in C) = 0.95 \text{ for all } \theta \in R$

If you repeat the experiment several times, you trap theta 95% of the time.

For Bayesians, on the hand, the probability is often a subjective belief. And parameters are random variables. They take the entire data intending to get the updated chance of the parameters.

$\\ p(\theta|X_1, ...., X_n) \propto \mathcal{L}(X_1, ...., X_n|\theta) * p(\theta) \\ \\ \text{Find the interval C such that } \int_C {p(\theta|X_1, ...., X_n)} d\theta = 0.95 \\ \\ \mathbb{P} (\theta \in C|X_1, ...., X_n) = 0.95$

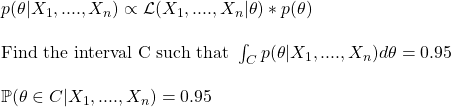
However, you will not trap the parameter 95% of the time if you repeat the experiment.

Related Posts