The word rationality has a different meaning in game theory than everyday usage. In common knowledge, rationality means the quality of a person seeking logic and reason for taking an action.
In game theory, the meaning is more specific and must fulfil a few conditions.
1) People are purposive: people engage in actions for an outcome. More specifically, the players involved in the game seek to achieve the most desired outcome.
2) Completeness of preference: the player’s preference order must be complete. For any two outcomes, X and Y, the player can choose X over Y, Y over X or indifferent between the two. But ‘I don’t know’ is not allowed! The following scheme represents the preference for X over Y:
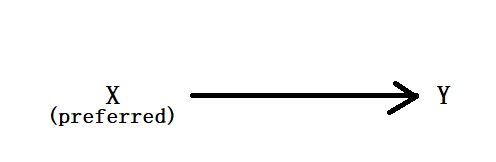
3) Transitivity of preference: For three outcomes, X, Y and Z, if X is preferred to Y and Y to Z, then X must be preferred to Z. So if a player prefers winning $1000 over winning $0. Winning $0 over not being able to participate, she must prefer winning $1000 over not being able to participate.
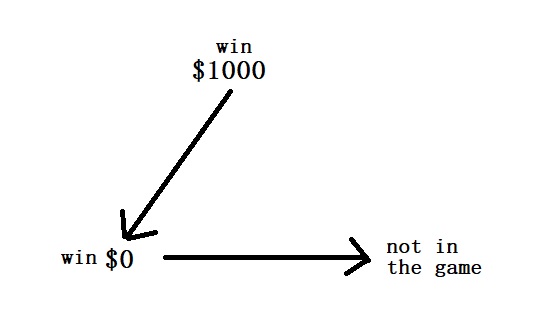
Implies
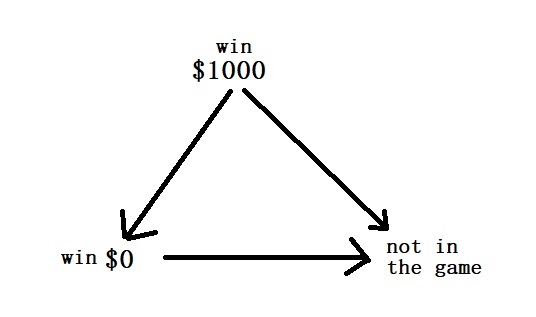
The preference ordering in this case is:
Win $1000
Win $0
Not in the game
4) Preference must be fixed
References
Rationality: David Hayes
Rationality: William Spaniel

