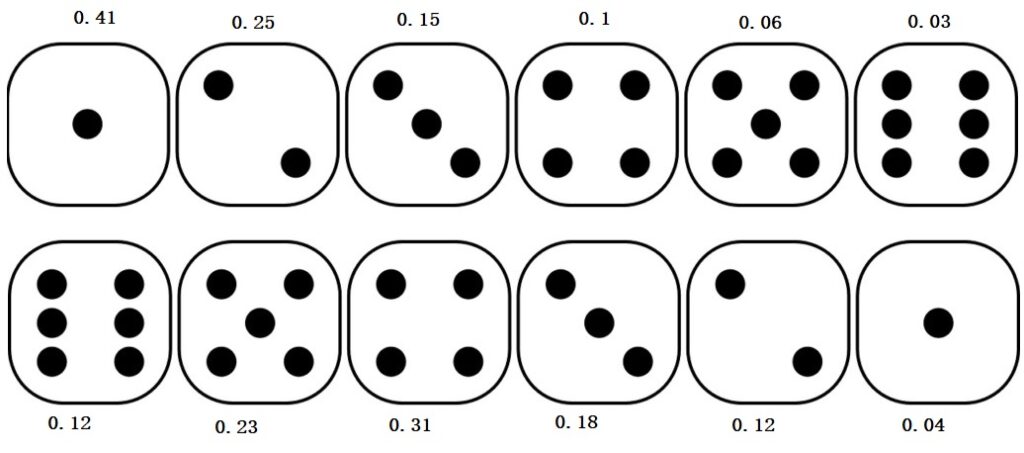
We have seen how the probability of double dice can be estimated by flipping and sliding the outcomes of the second die. Here is another example to illustrate the concept: this time, with two dice with different probabilities.
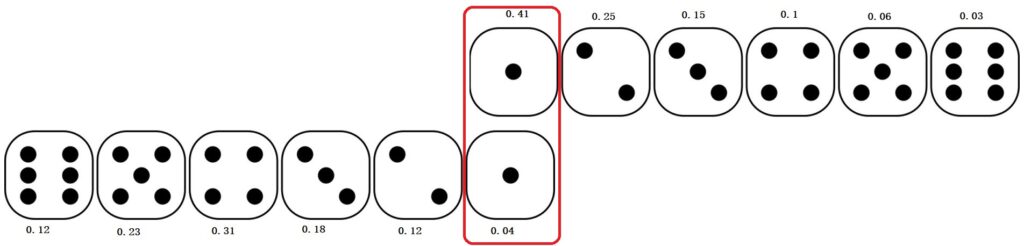
0.41 x 0.04 = 0.0164
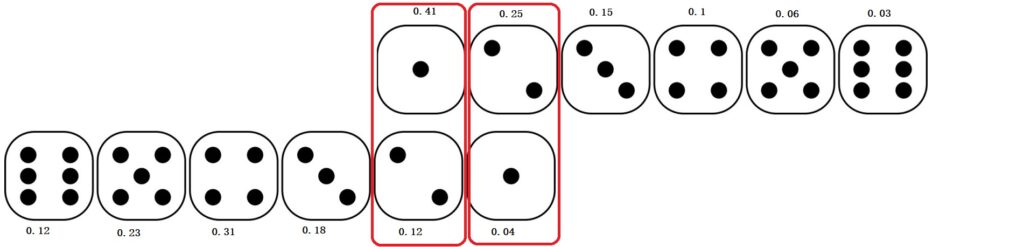
0.25 x 0.04 + 0.41 x 0.12 = 0.0592
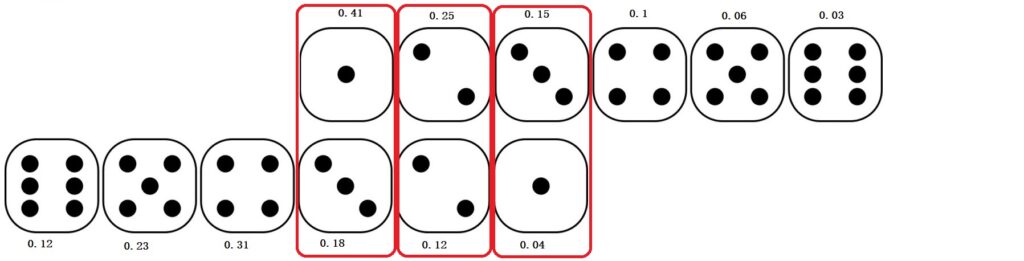
0.15 x 0.04 + 0.25 x 0.12 + 0.41 x 0.18 = 0.1098
Why X+Y in probability is a beautiful mess: 3Blue1Brown

