The answer to the birthday problem comes as a surprise to most of us. If you have not heard about this puzzle, you may read one of my earlier posts. At the same time, it is far less controversial than, say, the Monty Hall problem, as the former can be solved mathematically without much ambiguity.
A similar story on a Canadian lottery is narrated in the book The Drunkard’s Walk: How Randomness Rules Our Lives by Leonard Mlodinow. The officials have decided to give away 500 cars to 2.4 million of its subscribers using the unclaimed prize money of the past. They used a computer program to randomly pick 500 individuals and published the unsorted results, obviously not aware of the possibility of double-counting. And the result? One number was repeated, and a person got the car twice!
Let’s write an R code to numerically understand the probability of such an event to happen – a repeat of a number within 500, spread over 2.4 million. The program repeats a random number generation (the sample function), 500 at a time, 10000 times and averages it.
B<- 10000
n<- 500
results<- replicate(B, {
lot<- sample(1:2400000, n, replace=TRUE)
any(duplicated(lot))
})
mean(results)The program output, the probability of a repeat inside 500 numbers, is 5.4% – not an infinitesimally small number by any standard. The following plot shows how it grows with the sample size.
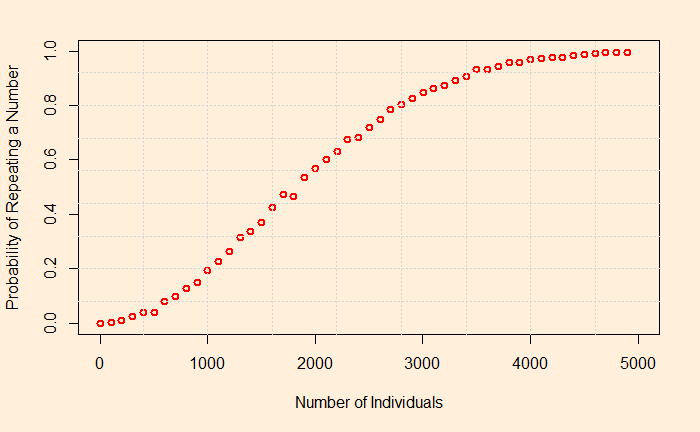
You will see that the repeat is almost certain before the number reaches about 4000.

