So, there is a 1/292201338 chance of winning a jackpot at the Powerball. That means if the prize is $20 million, the expected value of a ticket is $20,000,000 x 1/292201338 = $0.068. Not to forget, it includes the value to the individual and the state, which takes over half of the winning amount as taxes!

Consolation prizes
The jackpot is not the only thing you get; there are a few more things you win, as follows.
| Match | Prize |
| Five whites | $1,000,000 |
| Four whites + red | $50,000 |
| Four whites | $100 |
| Three whites + red | $100 |
| Three whites | $7 |
| Two whites + red | $7 |
| One white + red | $4 |
| Red | $4 |
Let’s look at the probabilities next.
Five whites and no red

P(5W AND NR) = P(5W)xP(NR)
P(5W) = 1 / 69C5 = 1/11238513
P(NR) = (25/26)
P(5W AND NR) = (1/11238513) x (25/26)
E.V. (5W AND NR) = $1,000,000 x 25 / (11238513 x 26) = $0.085
Four whites and One red

P(4W AND 1R) = P(4W)xP(1R)
P(4W) = How many ways of getting 4 winning numbers of 5 drawn out of all combinations of 5 from 69 = How many ways of getting 4 winning numbers of 5 drawn x How many ways of the remaining 1 is not / How many ways of getting 5 winning numbers of 5 drawn from 69 = (5C4 x 64C1) / 69C5 = 320 / 11238513
P(1R) = (1/26)
P(4W AND 1R) = (320/11238513) x (1/26)
E.V. (4W AND 1R) = $50,000 x (320/11238513) x (1/26) = $0.055
Four whites and no red

P(4W AND NR) = P(4W)xP(NR)
P(4W AND NR) = (320/11238513) x (25/26)
E.V. (4W AND NR) = $100 x (320/11238513) x (25/26) = $0.0027
Three whites and One red
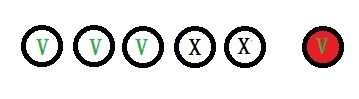
P(3W AND 1R) = P(3W)xP(1R)
P(3W) = (5C3 x 64C2) / 69C5 = 20160/ 11238513
P(1R) = (1/26)
P(3W AND 1R) = (20160/11238513) x (1/26)
E.V. (3W AND 1R) = $100 x (20160/11238513) x (1/26) = $0.007
Three whites and no red
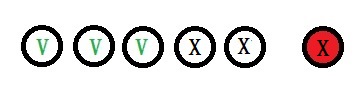
P(3W AND NR) = P(3W)xP(NR)
P(3W AND NR) = (20160/11238513) x (25/26)
E.V. (3W AND NR) = $7 x (20160/11238513) x (25/26) = $0.012
Two whites and One red
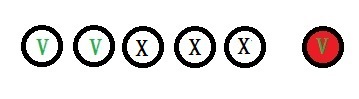
P(2W AND 1R) = P(2W)xP(1R)
P(2W) = (5C2 x 64C3) / 69C5 = 416640/ 11238513
P(1R) = (1/26)
P(2W AND 1R) = (416640/11238513) x (1/26)
E.V. (2W AND 1R) = $7 x (416640/11238513) x (1/26) = $0.01
One white and one red
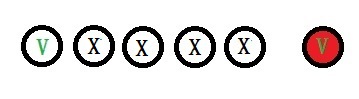
P(1W AND 1R) = P(1W)xP(1R)
P(1W) = (5C1 x 64C4) / 69C5 =3176880/ 11238513
P(1R) = (1/26)
P(1W AND 1R) = (3176880/11238513) x (1/26)
E.V. (1W AND 1R) = $4 x (3176880/11238513) x (1/26) = $0.04
Zero whites and One red
P(0W AND 1R) = P(0W)xP(1R)
P(0W) = (64C5) / 69C5 = 7624512/ 11238513
P(1R) = (1/26)
P(0W AND 1R) = (7624512/11238513) x (1/26)
E.V. (0W AND 1R) = $4 x (7624512/11238513) x (1/26) = $0.1
The Math of Powerball: Think Big
The odds you’ll win the Powerball jackpot: CNBC

