Portfolio theory is a simple theoretical framework for building investment mixes to achieve returns while managing risks. It used the concepts of expected values and standard deviations to communicate the philosophy.
Take two funds, 1 and 2. 1 has an expected rate of return of 12%, and 2 has 6%. On the other hand, 1 is more volatile (standard deviation = 6), whereas 2 is less risky (standard deviation = 3), based on historical performances. In one scenario, you invest 50:50 in each.
The expected value is 0.5 x 12 + 0.5 x 6 = 9%
To estimate the risk of the portfolio, construct the following matrix.

Omega values (1 and 2) are the proportions, sigmas are the standard deviations, and sigma12 is the covariance between 1 and 2. Substituting 0.5 for each omega (50:50) and noting that covariance is the product of the standard deviations x correlation coefficient, we get the following table for the two securities that are weakly correlated (correlation coefficient = 0.5),
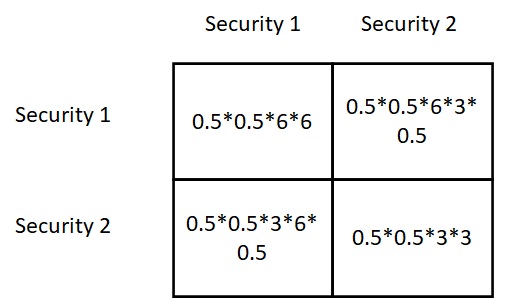
Add the entries in these boxes to get the portfolio variance. Take the square root for the standard deviation = 3.97.
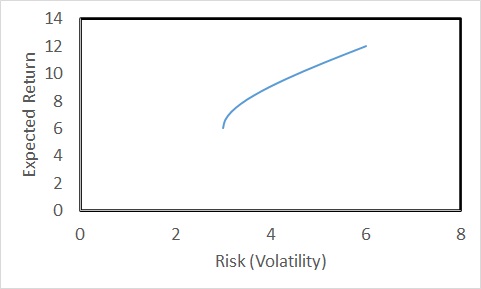
The expected rate of return of the portfolio is 9%, and the risk (volatility) is 3.97%. Continue this for all the proportions (omega1 = 1 to 0) and then plot the returns vs volatility; you get the following plot for a correlation coefficient of 0.5.
Imagine the securities do not correlate (coefficient = 0). The relationship changes to the following.
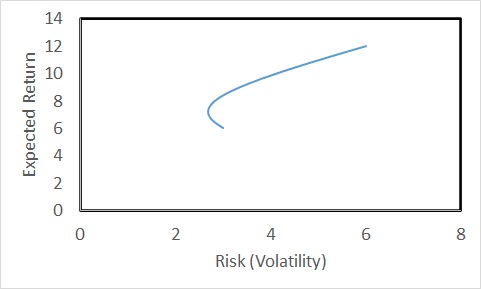
The risk is lower than the lowest (3%) for proportions of security1 less than 0.4. Even better, if the two securities are negatively correlated (correlation coefficient = -0.5),
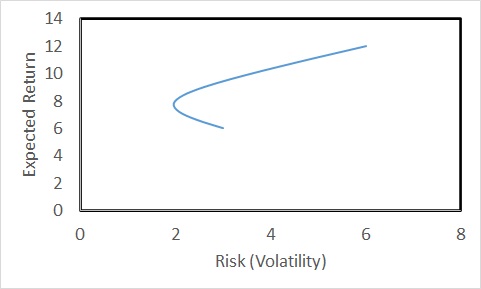
If there are n securities in the portfolio, you must create an n x n matrix to determine the variance.

