Raindrops are falling at a rate of 20 drops per inch per minute. What is the probability that no drop falls inside a 5-inch area for 3 seconds?
Since we consider the raindrops fall at random, we model this as a Poisson process. We need two parameters to estimate the required Poisson probability.
1) average rate of success: lambda
2) number of successes: s
Since we must consider zero success (s = 0) in a 3-second interval on a 5-inch area, we convert the success rate on the 5-inch area in 3 seconds.
lambda = 20 drops per inch per minute
= 20 x 5 = 100 drops per 5-inch area per minute
= 100/20 (= 5) drops per 5-inch area per 3 seconds
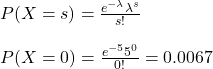
OR
dpois(0, 100/20)
