20% of mushrooms in a forest are red, 50% are brown, and 30% are white. A red mushroom has a 20% chance of being poisonous, whereas, for a non-red, it is 5%. What is the probability that a poisonous mushroom is red?
We have applied Bayes’ rule several times previously to solve similar problems. So straight to the equation.
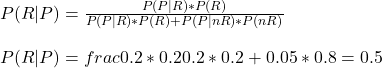
P(R|P) = Probability of red mushroom given that it is poisonous
P(P|R) = Probability of poisonous mushroom given that it is red = 0.2
P(R) = Prior probability of finding a red mushroom = 0.2
P(P|nR) = Probability of poisonous mushroom given that it is not red = 0.05
P(nR) = 0.5 + 0.3 = 0.8

