At a party of 25 people, how many handshakes are expected if each person asks hands with every other? Is this a permutation problem or a combination?
Before that, what is a permutation, and what is a combination? They both represent different ways of arranging things from an available list of options. For example, how many unique passcodes are possible for a combination lock of 4 wheels? Let’s count. There are ten possibilities for the first wheel (0-9), another 10 for the second, and the same for the third and fourth. Total possibilities = 10 x 10 x 10 x 10 = 104 = 10000. Some people will say there are 9999 ways, as one is always available to start!
Permutations
How many four-digit numbers can you make from 4, 6, 7 and 8? It is different from the combination lock problem as you can’t get to use it again once you use up one of the digits. So let’s do the counting: in the first place, you have four possibilities; in the second place, since one of them is used up, you have three, then two and finally, the remaining one. So the total permutatoins are 4 x 3 x 2 x 1 = 24.
Permutations of n available options taken r at a time = nPr. In the digit case, it was 4P4
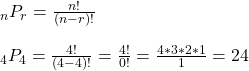
Combinations
The combination is where you make arrangements when the order does not matter. The handshake problem is a combination case. When two people shake their hands, one handshake happens. In other words, this becomes a permutation problem but discounting the double-counting. It is called combinations or nCr.
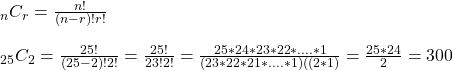
300 unique handshakes will happen.
Factorial Calculator

