It’s game theory time once again. Today, we’ll discuss strategic options available to layers while taking (and saving) football penalty kicks. In penalty kicks, the striker of the ball gets a chance to aim at the goal from about 11 m distance with only the goalkeeper to protect.

Since the reaction time is short, the goalkeeper must decide to judge the ball’s direction almost instantaneously, making the whole process a simultaneous game. Let’s build a payoff matrix reflecting such a game.
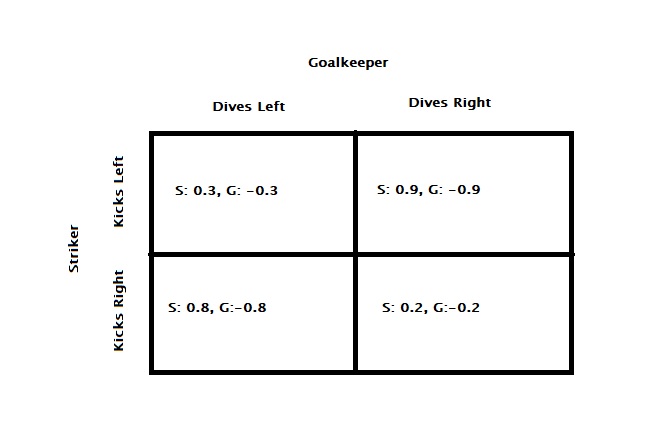
Before answering that question, we must know that the striker will randomise his shots, or it will hand a huge advantage over to the goalkeeper. And the goalie aims to make the striker indifferent to striking to the left vs the right. Then, find out the probability (for the goalkeeper to dive left) at which the striker’s payoffs are equal.
strike to left = strike to right
0.3*p + 0.9*(1-p) = 0.8*p + 0.2*(1-p)
(0.3 – 0.9 – 0.8 + 0.2)*p = 0.2 – 0.9
p = 0.7/1.2 = 0.58
The goalkeeper should try to dive left slightly more often. So, how many goals are expected in such a scenario? That is next.

