You may have heard about the Pareto principle or the 80:20 rule. It is used in several fields and sounds like: 80% of actions come due to 20% of reasons or 80% returns from 20% of efforts etc.
Pareto distribution is a form of power-law probability distribution used to describe several phenomena. In R, dpareto describes the probability density function and ppareto, the cumulative distribution function.
Let’s work out an example. Suppose the salaries of workers obey a Pareto distribution with a minimum wage of 1000 and the so-called shape factor, alpha = 3. What is the mean salary, and what is the percentage of people who earn more than 2000?
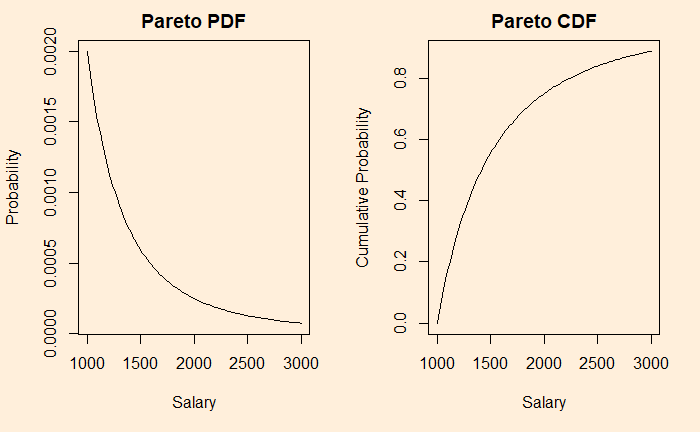
The Median is when the cumulative probability hits 0.5. So, applying the function for solving x such that ppareto(x, shape=3, scale=1000) = 0.5. x comes out to be 1260. For the answer to the other question, you find out the inverse of CDF (or 1 – CDF), i.e., 1 – ppareto(2000, shape=3, scale=1000) = 0.125 = 12.5%.

