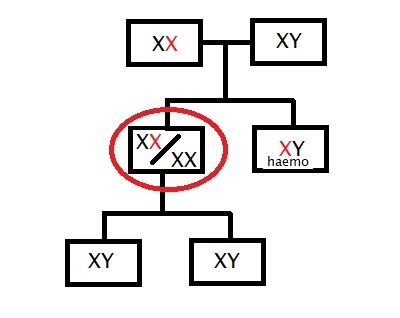
Here is a question. A lady has a brother who has haemophilia. Their parents did not have the disease, and her two sons also did not have any issues. What is the chance that the lady has a fine pair of X chromosomes? No other information.
Haemophilia is an inherited genetic disorder and is associated with X chromosomes. Typically, women have a low probability of having the condition as the likelihood of having errors in both the X chromosomes is low.
So, how do we work out the problem? The brother has haemophilia, which suggests that one X chromosome of their mother has the error. Why? Father can only give his Y to the son. Additionally, the father did not have the condition, suggesting his X was healthy. Now, the mother can pass the error or the error-free X to her daughter. So there are two chances: the lady has two healthy Xs (A) or one error X (notA). Since she has sons, their X must have come from her. The two children are unaffected (B).
The probability of two healthy sons if the lady has two healthy Xs, P(B|A) = 1. The chance of two healthy children if the lady has one unhealthy X, P(B|notA) is (1/2)x(1/2) = 1/4. P(A), the lady has healthy XX = (1/2) and P(notA), one unhealthy X = (1/2). We have everything. Call Mr Bayes.
The chance of the lady has a healthy XX, given that her two sons are healthy,
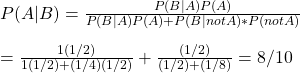
= 80%

