The ultimatum game continues between Annie and Becky. But there is a difference here.
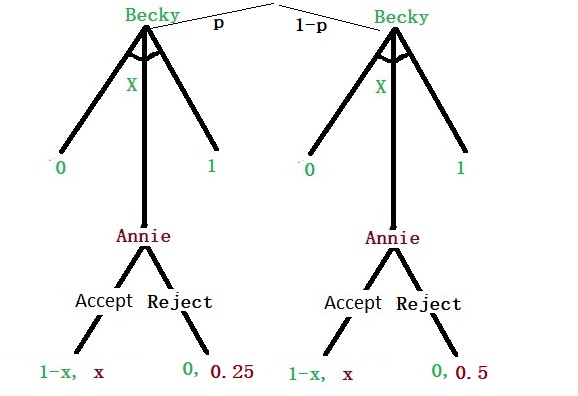
Like before, Becky is offering Annie a 0 to 1 division of the surplus, which Annie can accept or reject. However, instead of ending up with zero upon rejection, she has a payoff of 0.25 or 0.5 from an outside option. Unlike in earlier cases, Becky is uncertain about Annie’s bottom line. So, she attaches a probability p for 0.25 and (1-p) for 0.5. It means:
If Becky offers < 0.25, Annie rejects 100%
If Becky offers >/= 0.25 but < 0.5, Annie accepts with a probability p
If Becky offers >/= 0.5, Annie accepts 100%
If Becky offers 0.5, then her expected payoff is:
1 – 0.5 = 0.5
If Becky offers 0.25, then her expected payoff is:
p x (1-0.25) + (1-p) x 0 = 0.75 p
In other words, Becky should offer 0.25 if 0.75 p > 0.5 or p > 0.5/0.75 or p > 2/3
Bargaining 101 (#21): William Spaniel

