So how do you decide whether to choose one-tailed or two-tailed? It is not as straightforward as it may sound. Let’s look at the distributions that we have seen in the last post. So, first, the two-tailed test.
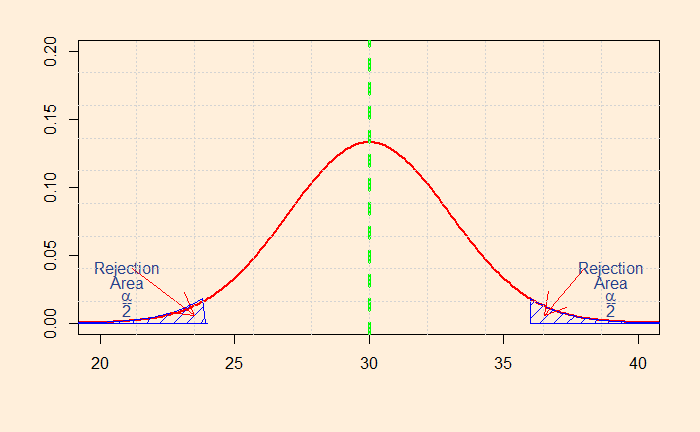
The shaded area represents the probability that a value will fall within the range. The smaller the value, you attain more confidence to reject the default – the null hypothesis. In this case, I have calculated the sum of the two regions to be 0.05. I guess you know what it means? It represents the alpha (significance level) of 5%.
Mean salary of 30k
So, if the null hypothesis (H0) was that the mean salary of engineers is exactly 30k, you can easily prove it is not the case if you find a sample mean of more than 35.9 or less than 24.1. Mathematically, it is:
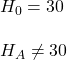
So far, so good.
What will you do if you decide to prove only the higher side of the claim? i.e., you want to establish that the salary is more than 30k. That will mean the following shaded area of the distribution.
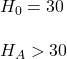
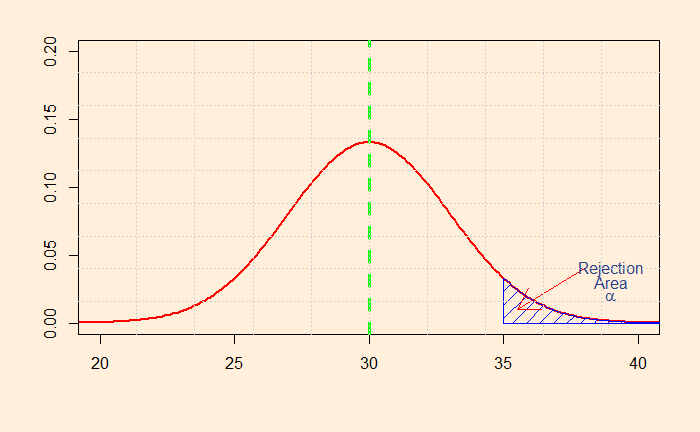
You can now see the problem: you can claim you have achieved the same 5% alpha at a sample mean of 35k.
In case you are wondering from where I got these 34.9, 24.1 and 35, try typing the following R codes.
pnorm(34.95, 30, 3, lower.tail = FALSE) # gives an answer 0.049 for one-tailed.
1 - pnorm(35.9, 30, 3) + pnorm(24.1, 30, 3) # gives 0.049 for two-tailed.
#the above code is equivalent to
pnorm(35.9, 30, 3, lower.tail = FALSE) + pnorm(24.1, 30, 3, lower.tail = TRUE)pnorm represents the cumulative density function of a normal distribution with a mean = 30 and the standard deviation = 3.

