Normal – Normal Sensitivity

In this fourth and final episode on the Bayesian inference with normal-normal conjugate pair, we find out how important is the choice for the prior and data collection in arriving at the answer. We will start from the previous set of inputs. But the relationship between the prior and the posterior first.

\\ \mu_{posterior} = \frac{\tau_0 \mu_0 + \tau \Sigma_{i=1}^{n} x_i}{\tau_0 + n*\tau} \\ \tau_{posterior} = \tau_0 + n*\tau \\ \sigma_{posterior} = \sqrt{\frac{1}{\tau_{posterior} }}

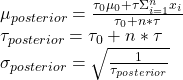
The parameters used in the first example are:

\\ \mu = \text {variable}; \sigma = 2 \text { (hypothesis)} \\ \mu_0 = 15; \sigma_0 = 4 \text { (prior)} \\ x = 9 \text{ (data)}

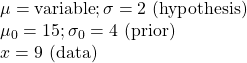
And the output is plotted below. The green curve is the prior probability distribution, blue represents the posterior in case of one data and red for 5 data (same value of 9). The vertical dotted line points at the data (or the average of the data).

It shows that (multiple) data at nine is pulling the distribution to come closer to it. Now let’s change the prior further right, mu0 = 25.

You see that the posterior distributions did not change much. Next, we will make the distribution narrower by defining sigma0 to be 2 and keeping mu0 at 25.

Things are now beginning to separate from the data. This suggests that if you want to be conservative with the estimation of posterior, it is better to keep the prior distribution narrower.

Finally, we check the impact of the standard deviation of the hypothesis. We change the value from 2 to 4, while keeping the original parameters as they are (mu_0 = 15; sigma_0 = 4):

Compare this with the first plot: you will see that making the hypothesis broader did not impact the mean value of the posterior.

Previous Posts on Normal-Normal

Normal-Normal conjugate
Normal-Normal and height distribution
Normal-Normal continued

Related Posts