We have seen how to come up with estimates of events based on assumed prior data using Bayesian inference. For discrete events that are rare, we have Poisson likelihood, and on such occasions, we use a Gamma prior and get a gamma posterior. In the same manner for Shaq, we found that the best one for estimating his success (or the lack of it) of entering Whitehouse is a binomial distribution. Once a data point is collected (one attempt), you update the chances using a beta distribution as a prior, and you get beta as the posterior.
Here is a new challenge you have a task to estimate the male height distribution of a particular country. We know from the examples of other countries that normal distributions describe the height distributions. A normal distribution has two parameters – mean and standard deviation, and our challenge is to estimate these parameters for our new country. We start with a set of hypotheses, use the available data and apply Bayesian inference to reach the goal.
Assume that I have collected data from the region, and it is 71 inches. Now I assume that the means ranges from 50 to 80 inches and the standard deviation from 1 to 4. Collect five hypotheses (purely random) from them as follows:
N(mean = 60, sd = 2), N(71, 3), N(65, 1.5), N(75, 4), N (80,1)
Now ask the question: what is the likelihood that my distribution of the new country is N(75, 4) given that I have collected data of 71 inches? Same for the rest four of the hypotheses. It can be estimated utilising the standard tables or using the R function dnorm(71, 75,4) = 0.06049268. The Pictorial representation is below.
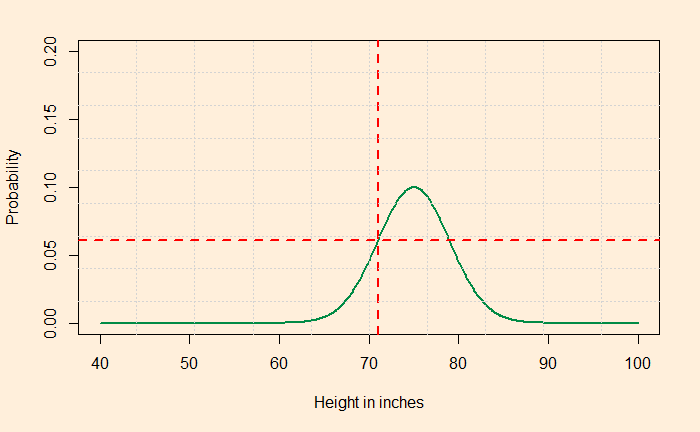
Before applying the Bayes’ theory, we should realise that 1) we need prior probabilities for each of the above five hypotheses and 2) we can have infinite hypotheses, not just five! Then we can apply the formula as we did before.
![]()
It is a conjugate problem (the prior will be a pdf), and the right prior is a normal distribution, making it a normal-normal problem. How to complete the exercise using normal-normal is something we will see next.

