Normal – Normal and Height Distribution

Continuing from the previous post, we will apply the normal-normal Bayesian inference to the height problem. The general format of the Bayes’ rule is:

$P(\text{height distribution}|height = 71)= \frac{Likelihood (height = 71|\text{a height distribution}) * P(\text{height distribution})}{\int Likelihood (height = 71|\text{a height distribution}) * P(\text{height distribution})}$

Since there are two parameters involved in the normal distribution, we have to have either a double integral in the denominator or choose one of the parameters, say the standard deviations, as known. So, we assume the standard deviation to be 4.0 in the present case. Let’s take the mean for the prior to be 69, the standard deviation to be 3 and see what happens. Therefore,

$\\ \mu = variable, unknown \\ \sigma = 4 \\ \tau = \frac{1}{\sigma^2} = 0.0625 \\ \mu_0 = 69 \\ \sigma_0 = 3 \\ \tau_0 = \frac{1}{\sigma_0^2} = 0.11 \\ \text{You will soon find out why I have defined }\tau$

Now we have everything to complete the problem.

$\\ \mu_{posterior} = \frac{\tau_0 \mu_0 + \tau \Sigma_{i=1}^{n} x_i}{\tau_0 + n\tau} = \frac{0.11 * 69 + 0.0625*71}{0.11 + 1*0.0625} = 69.72 \\ \\ \tau_{posterior} = \tau_0 + n\tau = 0.11 + 1*0.0625 = 0.1725 \\ \\ \sigma_{posterior} = \sqrt{\frac{1}{\tau_{posterior} }} = 2.4$

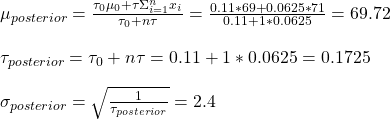
You can see a few things here: 1) the prior has moved a bit in the direction of the data but is still far from it, 2) the posterior is narrower than the prior.

Related Posts