There are three fair 6-sided dice with the following sides:
A. [2, 2, 4, 4, 9, 9]
B. [1, 1, 6, 6, 8, 8]
C. [3, 3, 5, 5, 7, 7]
If A plays against B, what is the probability of A winning?
A vs B
The required Probability is:
Probability of rolling a 2 x probability of 2 winning + Probability of rolling a 4 x probability of 4 winning + Probability of rolling a 9 x probability of 9 winning
= (2/6) x (2/6) + (2/6) x (2/6) + (2/6) x 1 = 20/36 = 55.55%
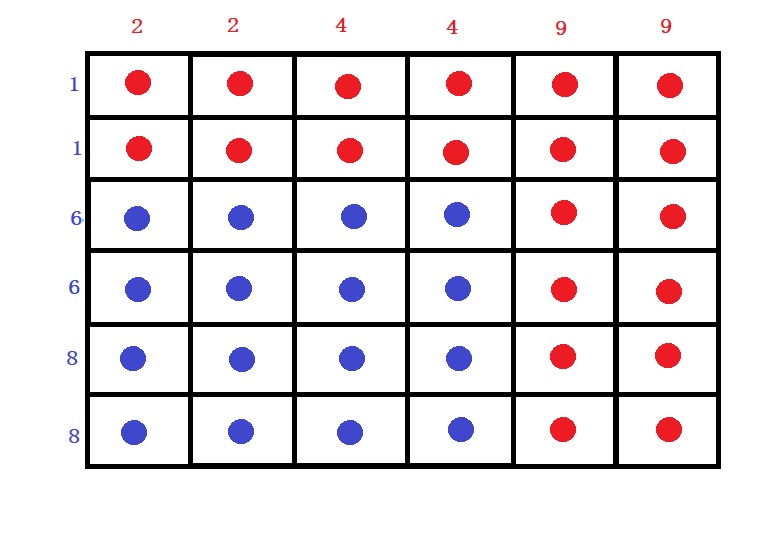
Count the number of red dots and divide it by the total number of dots.
What is the chance of B winning if B plays against C?
B vs C
= (2/6) x (0) + (2/6) x (4/6) + (2/6) x 1 = 20/36 = 55.55%
and
C vs A
= (2/6) x (2/6) + (2/6) x (4/6) + (2/6) x (4/6)= 20/36 = 55.55%
Each die beats the other with a probability of 55.55%.

