A usual tendency in regression is to chase better R-squared by increasing the dependent variables and ending up overfitting. Overfitting is a term used when your model is too complex that it sharts fitting noise. An example is this dataset taken from Regression Analysis Book by Jim Frost. It describes the highest approval ratings of the US presidents and their rank by historians.
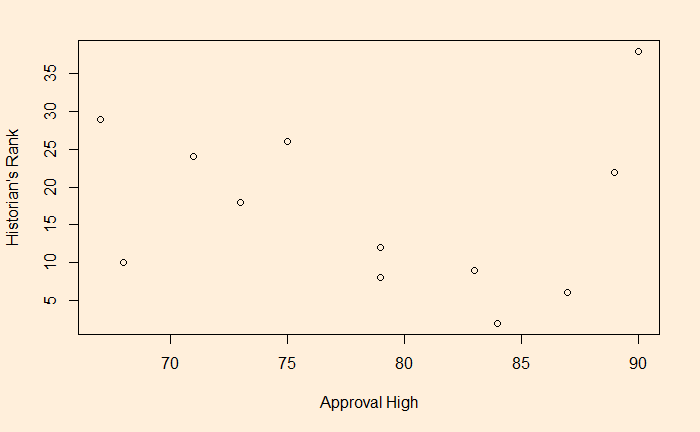
First, we try out linear regression and check the goodness of fit.
lm(Presi_Data$Historians.rank ~ Presi_Data$Approval.High)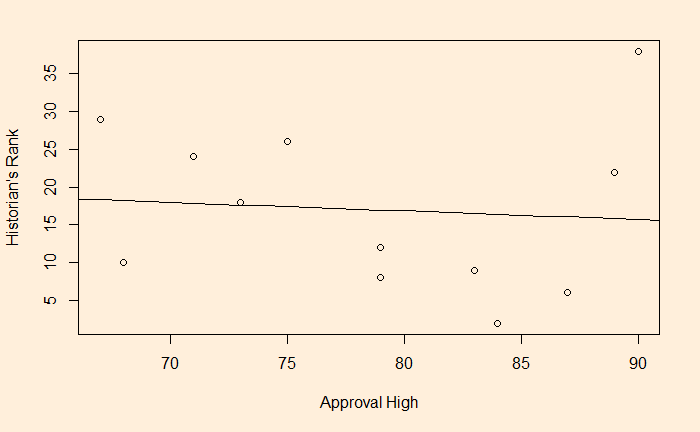
The R-squared value is close to zero (0.006766). Now, we try cubic fit.
model <- lm(Presi_Data$Historians.rank ~ Presi_Data$Approval.High + I(Presi_Data$Approval.High^2) + I(Presi_Data$Approval.High^3))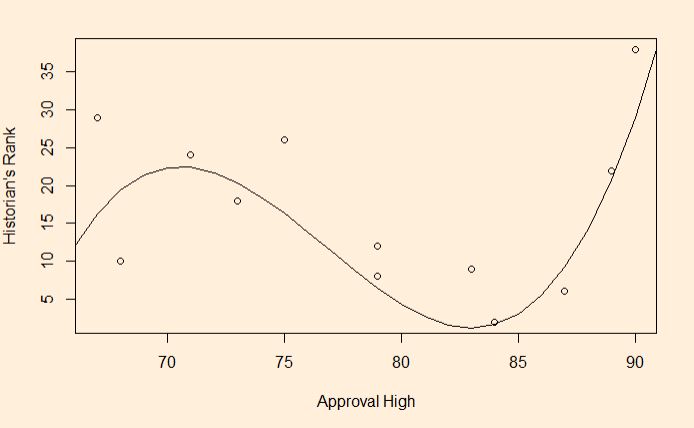
But with an impressive R-squared (0.6639)
Now, try thinking how one can explain this complex relationship, i.e. Historians Rank = -9811 + 388.9 x Approval High -5.098 x Approval High^2 + 0.02213 x Approval High^3!

