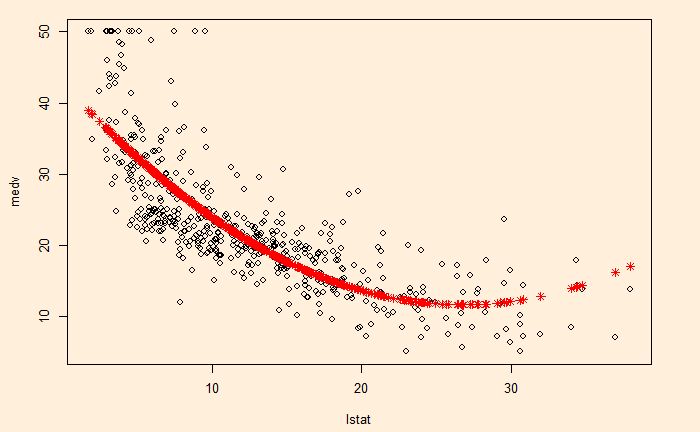
If you recall one of the previous posts relating ‘lstat’ with ‘medev’, we noticed the apparent curvature of the relationship. And how slightly awkward the fit-line on top of the scatter plot was.
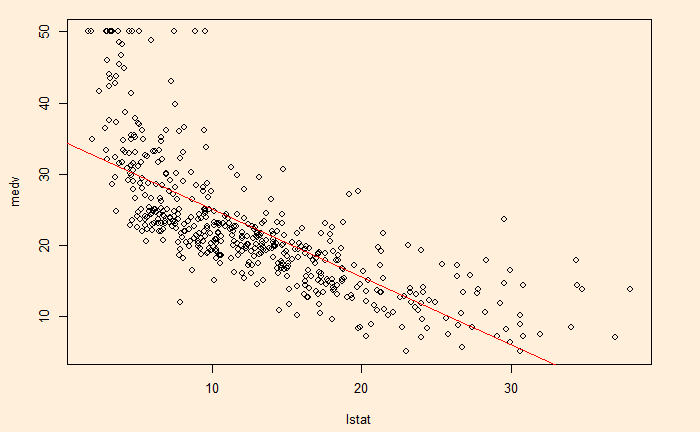
This seeming ‘non-linearity’ prompts us to extend the linear model to non-linear. We use a quadratic term by squaring the predictor (‘lstat’). We must use the identity function to do this.
fit5 <- lm(medv ~ lstat + I(lstat^2), Boston)The results are presented below:
Call:
lm(formula = medv ~ lstat + I(lstat^2), data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.2834 -3.8313 -0.5295 2.3095 25.4148
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42.862007 0.872084 49.15 <2e-16 ***
lstat -2.332821 0.123803 -18.84 <2e-16 ***
I(lstat^2) 0.043547 0.003745 11.63 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.524 on 503 degrees of freedom
Multiple R-squared: 0.6407, Adjusted R-squared: 0.6393
F-statistic: 448.5 on 2 and 503 DF, p-value: < 2.2e-16
Now, let’s compare the fit results.
plot(medv~lstat, Boston)
points(Boston$lstat, fitted(fit5), col = "red", pch = 8)