Multiple Linear Regression in R

We have seen linear regression before as a simple method in supervised learning. It is of two types – simple and multiple linear regressions. In simple, we write the dependent variable (also known as the quantitative response) Y as a function of the independent variable (predictor) X.

\\ Y \approx f(X) \\ \\ Y \approx \beta_0 + \beta_1 X

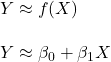
Beta0 and beta1 are the model coefficients or parameters. You may realise they are the intercept and slope of a line, respectively. An example of a simple linear regression is a function predicting a person’s weight (response) from her height (single predictor).

Multiple linear regression

Here, we have more than one predictor. The general form for p predictors is:

Y \approx \beta_0 + \beta_1 X_1 + \beta_2 X_2 + ... + \beta_p X_p

We use the Boston data set from the library ISLR2 for the R exercise. The library contains ‘medv’ (median house value) for 506 census tracts in Boston. We will predict ‘medv’ using 12 predictors such as ‘rm’ (average number of rooms per house), ‘age’ (proportion of owner-occupied units built before 1940), and ‘lstat’ (per cent of households with low socioeconomic status).

First, we do the simple linear regression with one predictor, ‘lstat’.

fit1 <- lm(medv~lstat, Boston)
summary(fit1)
Call:
lm(formula = medv ~ lstat, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.168  -3.990  -1.318   2.034  24.500 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 34.55384    0.56263   61.41   <2e-16 ***
lstat       -0.95005    0.03873  -24.53   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.216 on 504 degrees of freedom
Multiple R-squared:  0.5441,	Adjusted R-squared:  0.5432 
F-statistic: 601.6 on 1 and 504 DF,  p-value: < 2.2e-16

Here is the plot with points representing the data and the line representing the model fit.

fit1 <- lm(medv~lstat, Boston)
plot(medv~lstat, Boston)
abline(fit1, col="red")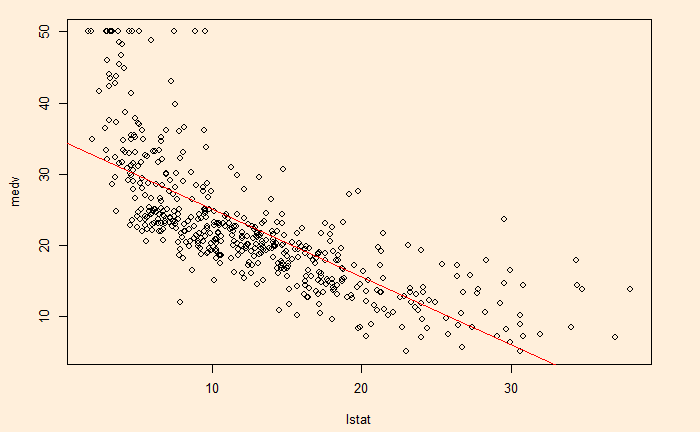

We will add another predictor, age, to the regression table.

fit2 <- lm(medv~lstat+age, Boston)
summary(fit2)
Call:
lm(formula = medv ~ lstat + age, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.981  -3.978  -1.283   1.968  23.158 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 33.22276    0.73085  45.458  < 2e-16 ***
lstat       -1.03207    0.04819 -21.416  < 2e-16 ***
age          0.03454    0.01223   2.826  0.00491 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.173 on 503 degrees of freedom
Multiple R-squared:  0.5513,	Adjusted R-squared:  0.5495 
F-statistic:   309 on 2 and 503 DF,  p-value: < 2.2e-16

beta_0 is 33.22, beta_1 is -1.03 and beta_2 is 0.034. All three are significant, as evidenced by their low p-values (Pr(>|t|)). We will add more variables next.

An introduction to Statistical Learning: James, Witten, Hastie, Tibshirani, Taylor

Related Posts