Adam finishes work at random times between 3 PM and 5 PM. His mother lives uptown, and his girlfriend lives downtown. After work, he goes to the metro station, catches the first train in either direction and has dinner with the person who lives on the side he reaches. His mother complains that his son came only two times in the last twenty working days, whereas Adam thought he was fair, with either party getting 50-50 chances. What’s really happening?
Suppose the metro on each side runs every 10 minutes, making it six times an hour: 3:00, 3:10, 3:20, etc. Let D represent the metro to downtown and U to uptown at x minutes after D.
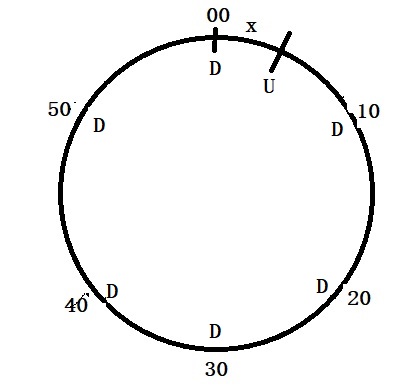
Since the mother saw him only twice in twenty days, the probability of Adam catching the uptown metro is 2/20 = 1/10, which must be equal to x/10. This implies x = 1. So the metro that goes uptown reaches its stop at 3:01, 3:11, 3:21, etc.
Reference
Fifty Challenging Problems In Probability: Frederick Mosteller

