In one of my previous posts, we have seen theoretical considerations of gambling with the roulette wheel. Today, we play the game not by going to a casino but by sitting behind a computer, using a simulation technique known as the Monte Carlo method.
Here, we let 1000 people play 100 games of each red/black betting. Starts with the players first:
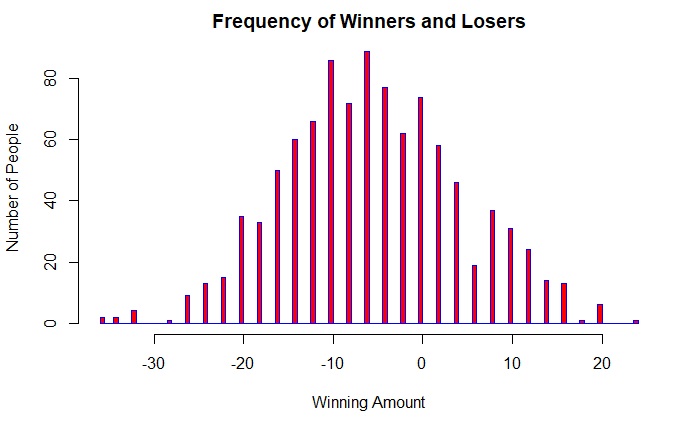
Approximately 250 people (25%) have won some money. Also, you don’t see the perfect distribution that you would have expected in a Bernoulli trial. This is because it is not a theoretical estimation but a real game using random numbers.
The Game is for Casino
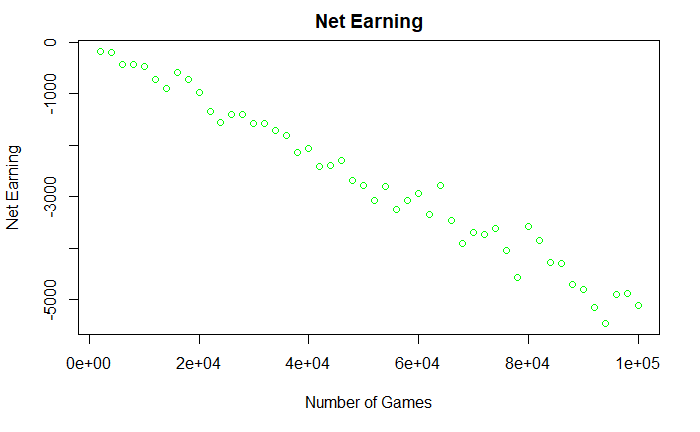
The rest of the post is about the casino owner. We know that the odds of a gambler winning colour is (18/38), and the odds of losing is (20/38) – about five cents per dollar net going the casino’s way. You will see from the picture that as the number of games increases, the certainty of getting 5 cents per dollar increases. It is sometimes known as the law of large numbers, where the actual value converges to the expected value as the number of events increases.
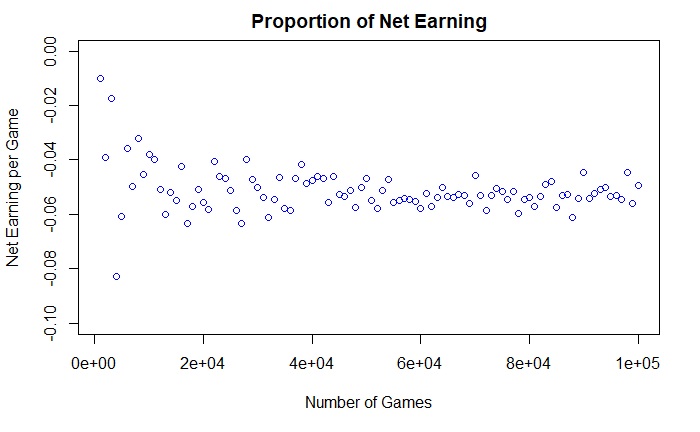
The next plot summarises the net money the casino earned in the day. Unless a few people turn up and play a really small number of games, the company would make what is expected: 5 cents per every dollar of value.
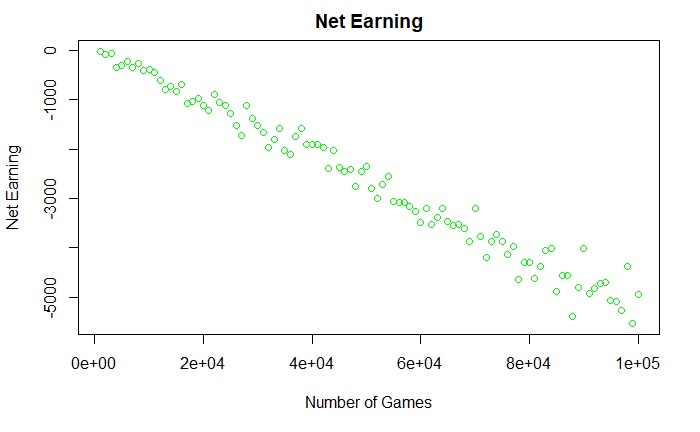
Now, let 2000 people play fewer (50) games each.
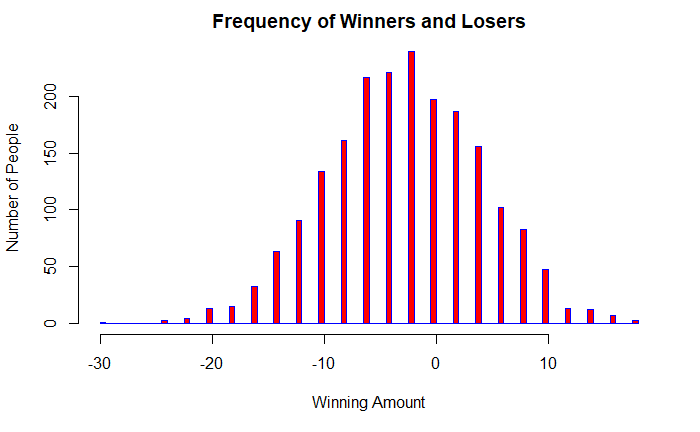
About 600 people out of 2000 (30%) may have won some money. As far as the Casino owner is concerned, he is pretty happy!