Memoryless Distribution

The exponential distribution is the time between two Poisson events. You may consider exponential distribution as the inverse of Poisson distribution. If the former is the events per time duration, the latter is the time per event. Since Poisson events are independent of each other, it should not be difficult to accept that the exponential distribution is called memoryless.

The following two plots may explain the inverse relationship. First is the Poisson PMF for events with parameter lambda = 5.

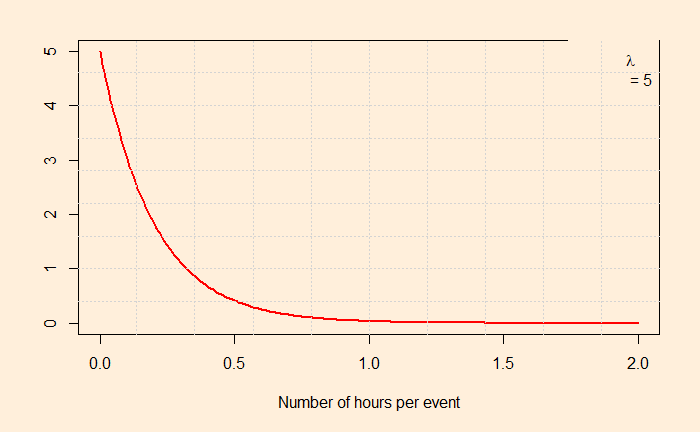
The next plot is the corresponding exponential distribution for the same lambda (5).

Memorylessness

We will look at the formal derivation of this memorylessness. First, what does a memoryless function mean? It means that the past segment of action has no impact on the subsequent segment. For example, the time required for a person to get a “one” of a die-roll (to enter a snake and ladder game) doesn’t depend on the previous 5 minutes that she had waited. Mathematically it means:

P(X > t + s | X > t) = P(X > s) \text { ; } t \text{ is forgotten!}

Let’s apply the Conjunction Rule, 

\\ P(A \cap B) = P(A) * P(B | A) \\ \\ P(B | A) = \frac{P(A \cap B)}{P(A)} \\ \\ \therefore P(X > t + s | X > t) = \frac{P(X > t + s \text{ } \cap \text{ } X > t) }{P(X > t)} \\ \\ \text{If } X > s + t \text{ , then } X > t \text{ is redundant} \\ \\ P(X > t + s | X > t) = \frac{P(X > t + s) }{P(X > t)} = \frac{e^{-\lambda(s+t)}}{e^{-\lambda(t)}} = e^{-\lambda s} \\ \\ \text{This is the definition of } P(X > s) \text{!}

Related Posts