Remember the cat-and-mouse game? We calculated the expected time for the mouse on door # 4 to reach the cat. As we know the Markovian technique, we will solve the problem using absorbing chains. Here is the situation with arrows representing the mouse’s stage-by-stage movement.

We follow the steps described in the previous post.
Step 1: Construct the transition probability matrix
Step 2: Isolate I and make Q
Step 3: Subtract Q from the Identity matrix
Step 4: Calculate the inverse of (I – Q)
In step 1, we re-arrange the columns and get the identity matrix cornered.

Q matrix is

And the rest of the calculations,
AA <- matrix(c(0, 0.5, 0, 0, 0,
0.5, 0, 0.5, 0, 0,
0, 0.5, 0, 0.5, 0,
0, 0, 0.5, 0, 0.5,
0, 0, 0, 0.5, 0), nrow = 5)
II <- matrix(c(1, 0, 0, 0, 0,
0, 1, 0, 0, 0,
0, 0, 1, 0, 0,
0, 0, 0, 1, 0,
0, 0, 0, 0, 1), nrow = 5)
BB <- II - AA
CC <- solve(BB)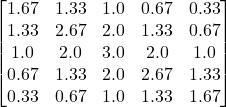
Add the elements of column 3, which represents door 4. It takes an average of 9 days for the mouse to be caught.
The Cats And Random Mouse Riddle: MindYourDecisions

