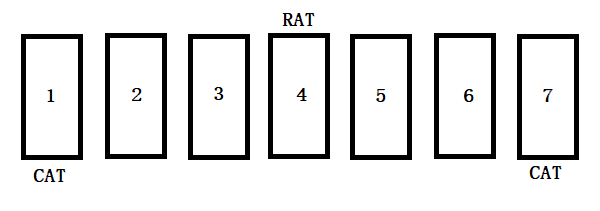
There are seven doors, and a mouse is at door 4. Two cats are waiting at door 1 and door 7. The rat moves one door in a day—either to the left or to the right. When it reaches the cat door, it gets eaten by the cat. What is the average number of days before the rat gets caught?
We can rename the arrangement since the mouse sits in the middle of the door sequence.
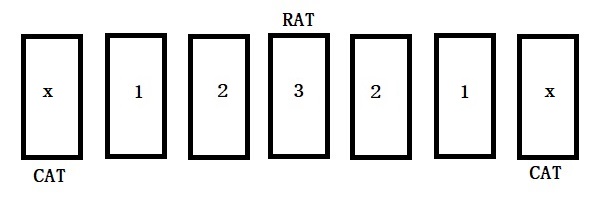
In the beginning, the mouse is at door 3, and let e3 be the expected time until the mouse gets caught by the cat. After one day, the mouse has a 50% chance of reaching the left or a 50% chance of reaching the right door. Either way, it reaches door 2 and lets e2 be the expected time until caught. Therefore,
e3 = 1 + e2
When the rat is one 2, after one day, the mouse has a 50% chance of reaching door 3 (waiting time e3) or a 50% chance of reaching door 1 (waiting time e1).
e2 = 1 + 0.5 e3 + 0.5 e1
From there, it either reaches door 2 or gets caught in a day.
e1 = 1 + 0.5 e2
Now, we have three linear equations to solve.
e3 = 1 + e2
e2 = 1 + 0.5 e3 + 0.5 e1
e1 = 1 + 0.5 e2
e2 = 1 + 0.5 + 0.5e2 + 0.5 e1
0.5 e2 = 1.5 + 0.5 e1
0.5 e2 = 1.5 + 0.5 + 0.25e2
0.25e2 = 2
e2 = 8
e3 = 1 + 8 = 9
e1 = 1 + 0.5 x 9 = 4
It takes an average of 9 days for the mouse to get caught.
The Cats And Random Mouse Riddle: MindYourDecisions

