Markov Chains – Absorbing chains

Let’s revisit the three stores. But there is a slight difference this time.

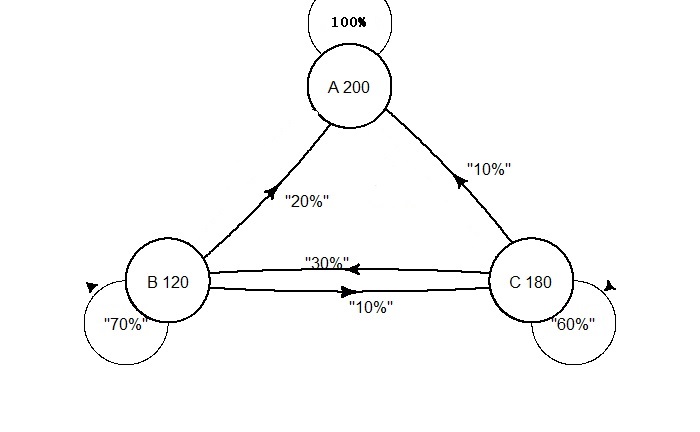
There is no arrow from store A to B or C. The customers who reach A are fully retained or absorbed. This is an absorbing Markov chain. The transition matrix for the above situation is,

$\begin{bmatrix} 1 & 0.2 & 0.1\\ 0 & 0.7 & 0.3\\ 0 & 0.1 & 0.6 \end{bmatrix}$

You may have guessed it already, but if you continue this chain to develop, the end-state distribution becomes,

$\begin{bmatrix} 1 & 0.2 & 0.1\\ 0 & 0.7 & 0.3\\ 0 & 0.1 & 0.6 \end{bmatrix} * \begin{bmatrix} A \\ B \\ C \end{bmatrix} = \begin{bmatrix} A \\ B \\ C \end{bmatrix}$

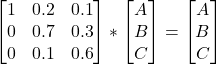
A + 0.2B + 0.1 C = A
0 + 0.7B + 0.3 C = B
0 + 0.1B + 0.6 C = C
A + B + C = 1

A + 1.2B + 1.1 C = 1
0 - 0.3B + 0.3 C = 0
0 + 0.1B - 0.4 C = 0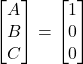

$\begin{bmatrix} A \\ B \\ C \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$

Eventually, all customers end up in store A.

Related Posts