The Markov approach is a concept for predicting stochastic processes. It models a sequence in which the probability of the following (n+1) event depends only on the state of the previous (n) event. Therefore, it is also called a ‘memoryless’ process.
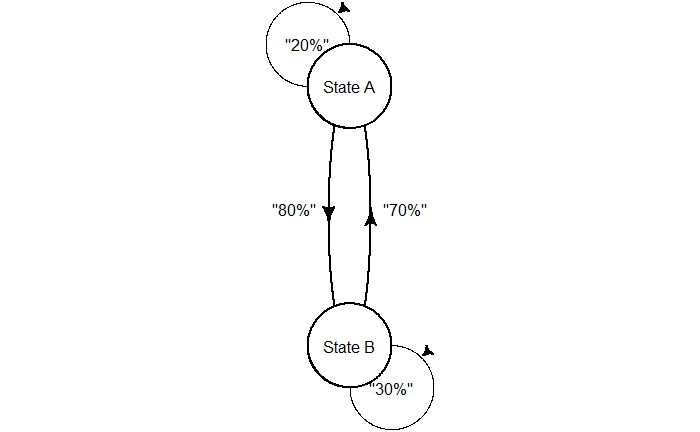
Before performing calculations, let’s familiarise ourselves with the concept and notations. Suppose there are two states: state A and state B. The process is expected to stay in the same stage for 20% of the time and can move to stage B in the remaining 80%. On the other hand, stage B has a 30% chance of staying and a 70% chance of moving to stage A. The following diagram depicts the process.
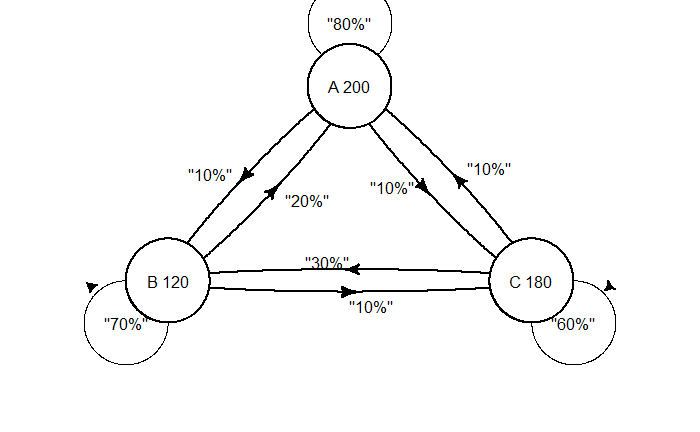
For example, imagine three shops in town—A, B, and C—that attract 200, 120, and 180 customers, respectively, this week. The following possibilities are expected for next week.
Shop A:
80% of the customers stay loyal
10% can move shop B
10% can move shop C
Shop B:
70% of the customers stay loyal
20% can move shop A
10% can move shop C
Shop C:
60% of the customers stay loyal
10% can move shop A
30% can move shop B
The question is, what is the expected number of customers in shops A, B, and C in the following week?

