Logistic Regression and R

We have seen logistic regression as a means to estimate the probability of outcomes in classification problems where the response variable has two or more values. We use the ‘Default’ dataset from ‘ISLR2’ to illustrate. The data set contains 10000 observations on the following four variables:

default
: A factor with levels No and Yes indicating whether the customer defaulted on their debt

student:
 factor with levels No and Yes indicating whether the customer is a student

balance: 
The average balance that the customer has remaining on their credit card after making their monthly payment

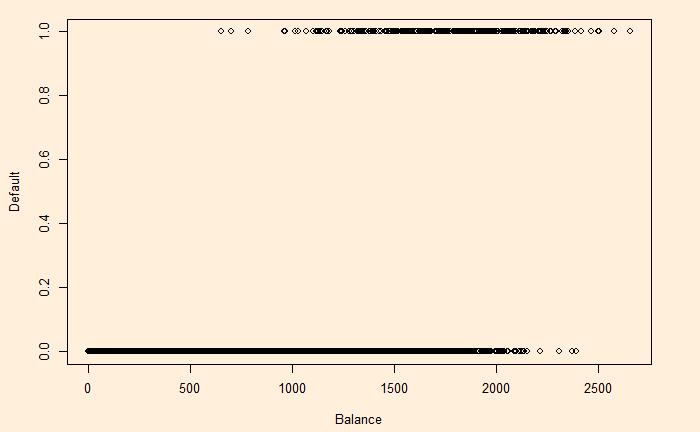
income: Income of customer

We change YES to 1 and NO to 0 and plot default vs balance.

Let p(X) be the probability that Y = 1 given X. The simple form that fits this behaviour is:

The beta values (the intercept and slope) are obtained by the ‘generalised linear model’, glm function in R.

D_Data <- Default
D_Data$def <- ifelse(D_Data$default=="Yes",1,0)
model <- glm(def ~ balance, family = binomial(link = "logit"), data = D_Data)
summary(model)

Call:
glm(formula = def ~ balance, family = binomial(link = "logit"), 
    data = D_Data)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.2697  -0.1465  -0.0589  -0.0221   3.7589  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -1.065e+01  3.612e-01  -29.49   <2e-16 ***
balance      5.499e-03  2.204e-04   24.95   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 2920.6  on 9999  degrees of freedom
Residual deviance: 1596.5  on 9998  degrees of freedom
AIC: 1600.5

Number of Fisher Scoring iterations: 8

Now, we will test how good the model predictions are by plotting the function using the regressed beta₀ ( = -10.65) and beta₁ (= 0.0055).

plot(D_Data$balance, D_Data$def, xlab = "Balance", ylab = "Default")

y <- function(x){
  exp(-10.65+0.0055*x) / (1 + exp(-10.65+0.0055*x))
}

x <- seq(0, 3000)
lines(x, y(x), col = "red")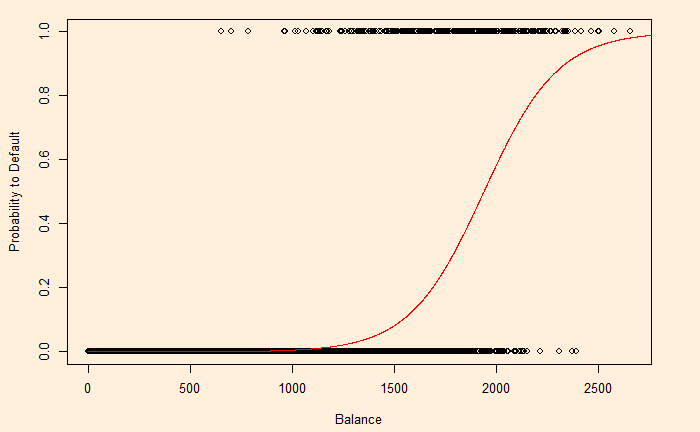

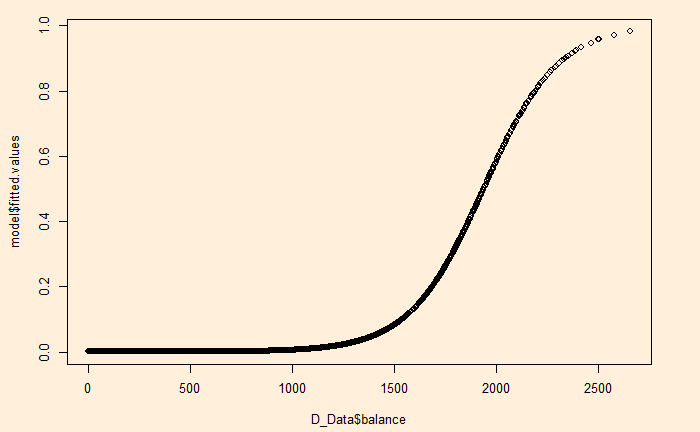
But R has an even simpler way to get this curve.

plot(D_Data$balance, model$fitted.values)