A factory makes two products, Alpha and Beta, using four ingredients: A, B, C and D. The quantity requirement for each component per kg of the product is:
| A | B | C | D | |
| Alpha | 500 | 750 | 150 | 200 |
| Beta | 500 | 625 | 100 | 300 |
The profits from the products (per kg) are
| Profit | |
| Alpha | 45 |
| Beta | 50 |
The maximum daily demands for the product (kg) are:
| Profit | |
| Alpha | 50 |
| Beta | 20 |
If there are constraints (as below) on the supply of the ingredients, what should be the product mix?
| A | B | C | D |
| 20000 | 42000 | 10400 | 9600 |
Linear Programming
This is an example of the application of linear programming (LP), a popular tool in prescriptive analysis. The solution starts by identifying the decision variables and the objective function.
The quantities of the two products are the decision variables. Let’s name them X1 (alpha) and X2 (beta). The objective (function) is to maximise the profit, 45 X1 + 50 X2. All the other information provided above are constraints (on the ingredients, demand, etc). The LP formulation is given below:
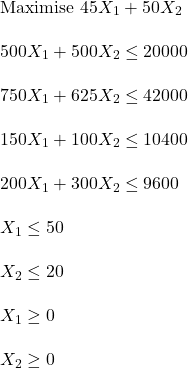
We use R to solve the set of equations. The package used is ‘lpSolve’.
library(lpSolve)
f.obj <- c(45, 50)
f.con <- matrix (c(500, 500, 750, 625, 150, 100, 200, 300, 1, 0, 0, 1), nrow = 6, byrow = TRUE)
f.dir <- c("<=", "<=")
f.rhs <- c(20000, 42000, 10400, 9600, 50, 30)
results <- lp ("max", f.obj, f.con, f.dir, f.rhs)
results
results$solutionSuccess: the objective function is 1880
24 16The maximum profit is 1880, and the optimal production quantities are alpha = 24 and beta = 16.

