Random processes are far mischievous than you could ever imagine. It is partly due to the inability of our minds to correctly understand randomness in real life. Yes, it is easy to follow in classrooms – those head and tail stuff. If I toss a coin once, I get 100% of an outcome, irrespective of its theoretical probability of occurrence of 0.5, piece of cake! It is easy for us to acknowledge the gambler fallacy or the theory of large numbers.
Yet, when it comes to real life, especially when it comes to rare events, we forget all we have learned and become captains of the ship of irrationality. Today we take an example, which is the favourite of reporters and cherry-pickers.
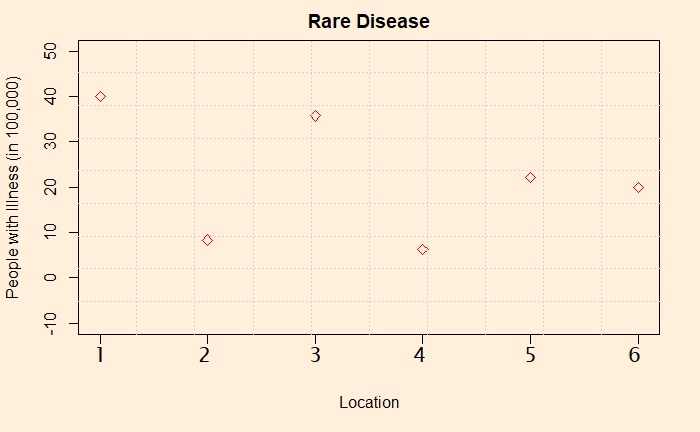
Consider this: you are working in the city centre, and want to live in one of its suburbs – place1. Your friend comes to know about your decision, and she shows you a newspaper article that talks about the stats on a rare disease. She recommends place2 or place4 as she thinks place 1 has four times more prevalence of the disease.
You are not happy, and you find out the population of those places – They are between 10,000 to 20,000. You then collect data on the disease from more parts of the world and find the following.
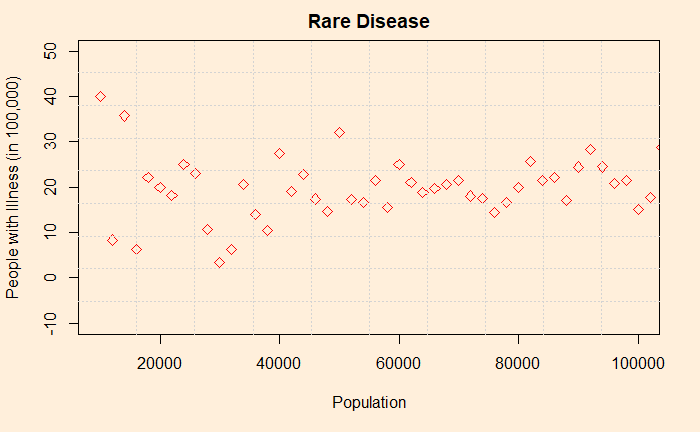
You are more interested now, and you refer to the standard statistics textbook and read about binomial trials. You make an assumption, based on the data points towards the right-hand side and decide that the mean value is 20 per 100,000 population. Then finds two formulae for random variables that followed binomial distributions (Bernoulli).
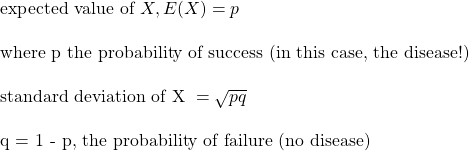
You assume E(X) to be 20/100,000 and patiently estimate the standard deviation and then standard error (by diving with the square root of population) for populations from 10,000 to a million. And generate a plot of a 95% confidence interval. Don’t know how to estimate confidence intervals? Check this out.
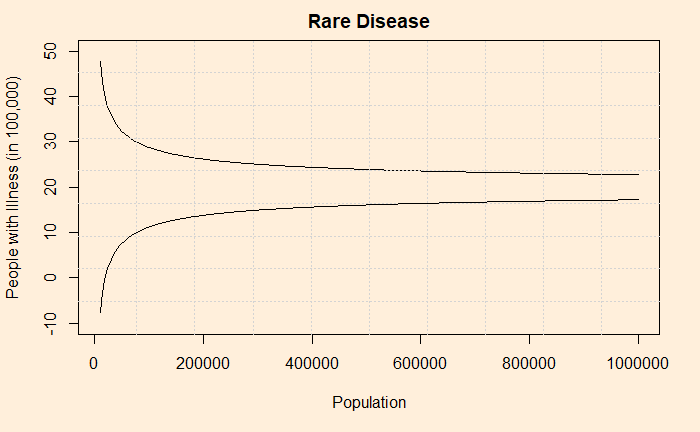
In the whole of this exercise, you used only a single number for the disease probability but got a funnel-like plot! Now you get more data from all over the world and they fit inside the funnel.
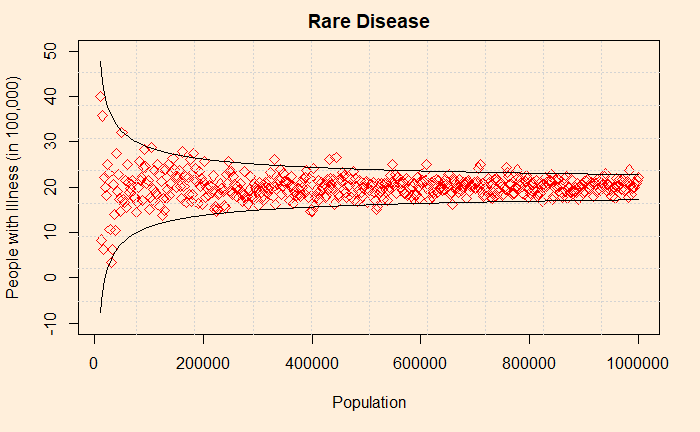
What are your conclusions?
1) There is nothing wrong with any of those six places – at least regarding this rare disease.
2) People make the mistake of misinterpreting randomness in smaller populations all the time.
3) One reason is lack of knowledge.
4) The other reason is fundamental to our species; its complete surrender to two emotions – fear and greed. It was greed that made you a bankrupt chasing gambler fallacy. This time, it is the fear of disease, which made you forget your basics.
Further reading
The art of statistics: Learning from Data: David Spiegelhalter

