Before analysing inequality, let’s develop an intuition. Suppose the profit from sales of an object moves the following way with the price.
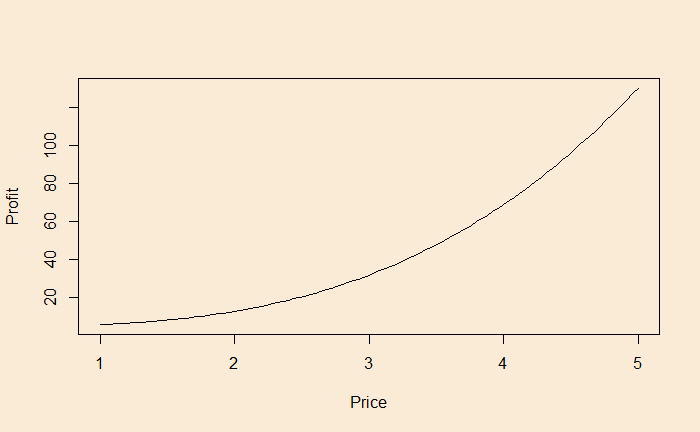
The price can be 2, 3, or 4 in a given year with equal probabilities. What is the average profit?
The mathematical function that presents the above behaviour is x3 + 5. Suppose the price values (x) 2, 3, and 4 can occur equally likely. This means the average price value is (2+3+4)/3 = 3. The profit at x = 3 is 33+5 = 32.
Let’s estimate the profit at each x value and then take the average.
at x = 2, profit = 23+5 = 13
at x = 3, profit = 33+5 = 32
at x = 4, profit = 43+5 = 69
Average is (13+32+69)/3 = 38
This is Jensen’s inequality, which says that the average (expected values) of inputs do not lead to average output if the function is non-linear. Depending on the shape of the non-linearity, it can under-estimate or over-estimate.

