IQ Power

Let’s assume the IQ of a population is normally distributed with a standard deviation of 16. A hypothesis test collected 16 samples for the null hypothesis of mean IQ = 100 for a significance level of 5%. What is the power of the hypothesis test if the true population mean is 108?

Definition: The power of a test is the probability that it will correctly reject the null hypothesis when the null hypothesis is false.

Step 1: Estimate the Z-score for the alpha (significance level)

qnorm(0.05, 0, 1, lower.tail = FALSE)

1.645

Step 2: Estimate IQ corresponds to Z = 1.645

$\\ Z = \frac{\hat{X} - \mu}{\sigma/\sqrt{n}} \\ \\ \hat{X} = \frac{Z \sigma}{\sqrt{n}} + \mu$

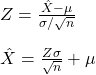
1.645 * 16 / sqrt(16) + 100 =  106.58

Above the IQ average of 106.58, the Null hypothesis (that the mean = 100) will be rejected.

Step 3: Estimate Z-score at X = 106.58 for mean = 108

$Z = \frac{106.58 - 108}{16/\sqrt{16}} = -0.355$

The entire area above Z = -0.355 is included in the power region (the area below Z = -0.355 will be the false negative part as the null hypothesis will not be rejected).

Step 4: Estimate the cumulative probability > Z = -0.355

pnorm(-0.355, 0, 1, lower.tail = FALSE)

 0.639

The power is 0.639 or 64%

Reference

Power Functions: PennState

Step 1: Estimate the Z-score for the alpha (significance level)

Step 2: Estimate IQ corresponds to Z = 1.645

Step 3: Estimate Z-score at X = 106.58 for mean = 108

Step 4: Estimate the cumulative probability > Z = -0.355

Reference

Related Posts