Last time, we have seen how the choice of prior impacts the Bayesian inference (the updating of knowledge utilising new data). In the illustration, a well-defined (narrower) distribution of existing understanding more or less remained the same after ten new, mostly contradicting data.
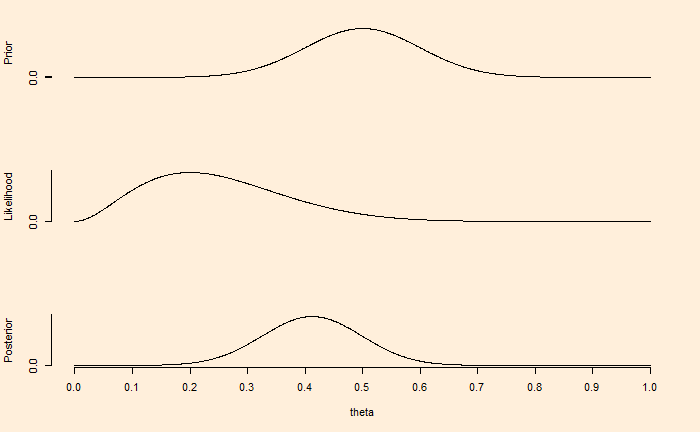
Now, the same situation but collected 100 data, with 80% leading to tails (the same proportion as before).
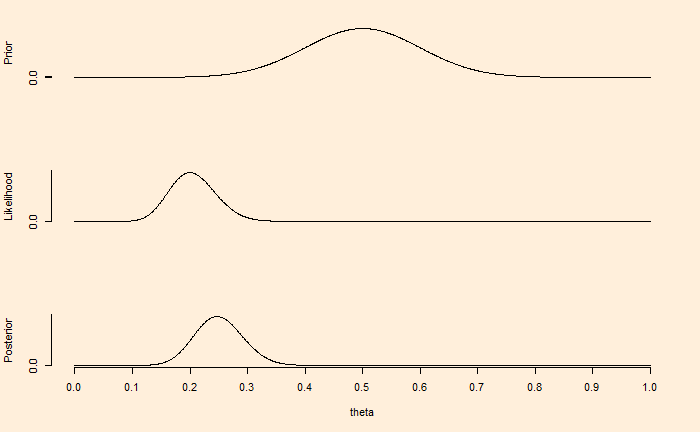
Now, the inference is leaning towards new compelling pieces of evidence. While Bayesian analysis never prohibits the use of broad and non-specific beliefs, the value of having well-defined facts is indisputable, as illustrated in these examples.
If there are multiple sets of prior available, it is prudent to check their impact on the posterior and map their sensitivities. Sets of priors can also be joined (pooled) together for inference.

