See a game played between two rational players with the following payoff matrix.
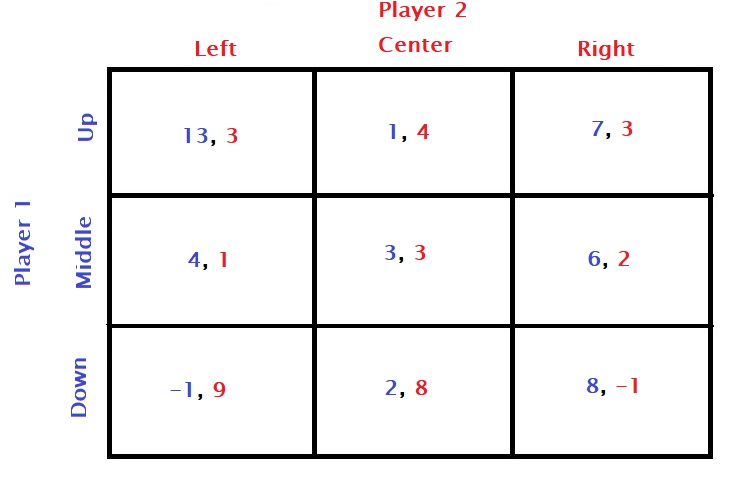
Looking at the matrix, one can see that player 2 is unlikely to choose the right strategy as her payoffs, 3, 2 and -1, are worse off against left and centre. So for player 2, the matrix is the following.
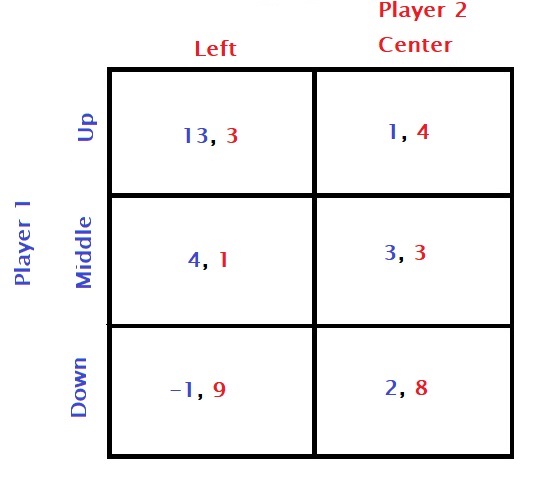
Player 1 knows what Player 2 is thinking because she is also rational. She looks at her options and concludes that down is no longer an option for her (- 1 < 4 and 2 < 3). So he eliminates the row corresponding to down.
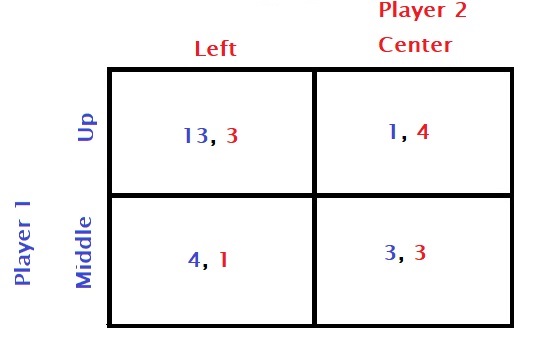
Player 2 knows that the option down is the least favourite to Player 1, so she compares options left and centre. Centre dominates (4 > 3 and 3 > 1).
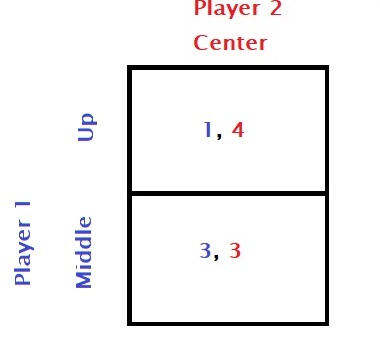
If that is the case, Player 1 will choose the middle, which gives her a better incentive.
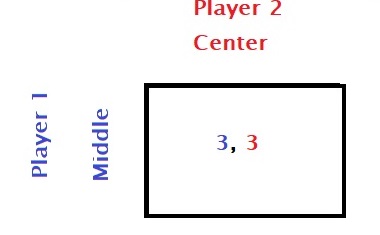
The whole game structure is common knowledge between the two players. Such games are known as iterated elimination of strictly dominated strategies or IESDS.

