The rules of roulette appear complex, with so many types of bets and payoffs. We have seen the basic odds of roulette in an older post, and this time we spend time demystifying the complexity. First, look at the wheel (American roulette).

And the layout on which the player places the bet is:
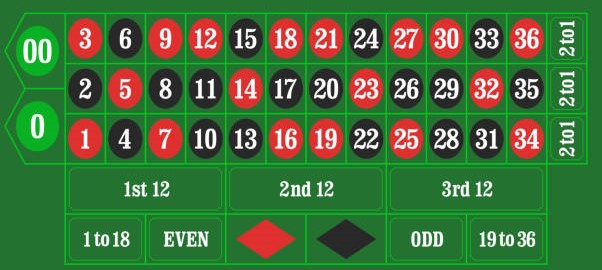
Now, various possible bets and payoffs.
| Bet | Explanation | numbers covered | Payoff |
| Straight | the bet covers a number | 1 | 35 to 1 |
| Split | bet on two adjacent numbers on the layout | 2 | 17 to 1 |
| Street | bet on a column of 3 numbers (e.g. 12, 11, 10) | 3 | 11 to 1 |
| Corner | any block of 4 numbers of 2 x 2 (e.g. 32, 35, 31, 34) | 4 | 8 to 1 |
| Basket | five number combination of 00, 0, 3, 2, 1 | 5 | 6 to 1 |
| Double Street | 2 adjacent columns of the layout; a bet covers 6 numbers | 6 | 5 to 1 |
| A dozen | 1-12, 13-24 or 25-36, by placing a bet on one of the 3 locations of the layout | 12 | 2 to 1 |
| Even-money | odd/even, red/black, low (1-18), high (19-36) | 18 | 1 to 1 |
Now, forget everything and let’s find out how payoffs are made, and what the expected values are.
Expected Value, E
The expected value of a random variable is a weighted average. In other words, you take the value of each variable, multiply it by its probability to occur and sum over all the variables. Imagine a coin-tossing game – you get one dollar for a head and lose 1 for a tail. The outcomes hear and tails, are random variables, each with a chance of 1 in 2 (0.5). So, the expected value = P(H) x V(H) + P(T) x V(T) = (1/2)x(1) + (1/2)(-1) = 0. Or, if you play the game over and over, you are expected to gain (or lose) nothing, but you should play for a long time to see that outcome. I have used V to denote value.
Another example: you play 6-sided dice. You get 6 dollars if the dice rolls on 3, and lose 1 dollar for everything else. The expected value (if you play long enough) is E = (1/6)(-1) + (1/6)(-1) + (1/6)(6) + (1/6)(-1) + (1/6)(-1) + (1/6)(-1) = (6/6) – (5/6) = 1/6. So, keep playing.
Roulette
We have seen how it works in Casino games. We will formalise it this time. Look carefully at the last two columns of the bet-payoff table, and you can make a formula payoff = (36 – numbers covered ) / numbers covered. The formula holds good except for Basket, where the answer is (36-5)/5 = 6.2, but the casino rounds it off to 6 (benefits who?).
Let N be the number of pockets on the wheel (38 for American and 37 for European), and n be the number covered. The chance of getting one number from 38 possibilities is (1/38). The probability of getting one out of two numbers (such as a split) is (1/38) + (1/38) = 2/38 – remember the addition rule of mutually exclusive events? So the generalised formula for getting one number in a bet that covers n numbers is n/38, and the expected value is
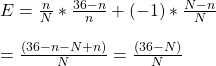
There is something special about the final equation – that it is independent of the numbers covered but depends only on the number of pockets on the roulette wheel. In other words, if the game has a smart payoff structure given by a formula (36 – numbers covered ) / numbers covered, you get a bet-independent payoff (or a constant payoff).
House wins, always
We will plug in numbers and find out the advantage – you already know it’s a house advantage for any N more than 36. So for the American, it is (36-38)/38 = – 0.0526 or 5.26%; for the European, it is (36-37)/37 = – 0.027 or 2.7%. The Basket doesn’t exactly fit the rule, and its house advantage is higher at 7.89%.

