You know, your friends, on average, have more friends than you do! I know it is a bit difficult to swallow that feeling. We will explore it mathematically. On the one hand, it follows from what we have seen before – the inspection paradox and the waiting-time paradox. But we will use a different approach here.
Count your friends
Consider the following relationship tree.
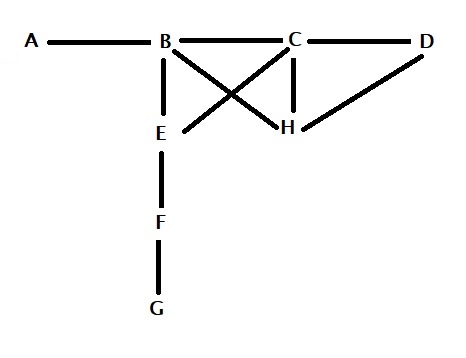
What it means is that A has only one friend (i.e., B) denoted by A(1; B). Similarly B(4; A, C, E, H), C (4; B, D, E, H), D(2; C, H), E(3; B, C, F), F(2; E, G), G(1; F), H(3; B, C, D). So the total number of friends among those eight is 1 + 4 + 4 + 2 + 3 + 2 + 1 + 3 = 20. The average number of friends, therefore, is 20/8 = 2.5.
And their friends
How do we do it? The easier way is to call out each of them and ask how many friends they have. For example, take A: she will ask her only friend, B, to call out her friends. B has four friends (note that it also includes A). Let us represent that as A{B(4)}. Similarly, B{A(1), C(4), E(3), H(3)}, C {B(4), D(2), E(3), H(3)}, D{C(4), H(3)}, E{B(4), C(4), F(2)}, F{E(3), G(1)}, G{F(2)}, H{B(4), C(4), D(2)}. The total number is 60. To calculate the average friends’ friends, you should divide 60 by the friends you calculated earlier, i.e., 20. 60/20 = 3.
So by counting, you prove that the average number of friends (2.5) is smaller than friends’ friends (3). The whole exercise can be summarised in the following table
| Individual | Friends (P) | Friends’ friends (Q) | Mean Friends’ friends (P/Q) |
| A | 1 | 4 | 4 |
| B | 4 | 11 | 2.75 |
| C | 4 | 12 | 3 |
| D | 2 | 7 | 3.5 |
| E | 3 | 10 | 3.33 |
| F | 2 | 4 | 2 |
| G | 1 | 2 | 2 |
| H | 3 | 10 | 3.33 |
| Total | 20 | 60 | 23.91 |
Analytical Proof

Look at the diagram once more. We replace the number of friends that A have with dA (dA represents the degree of the vertex that points from person A).
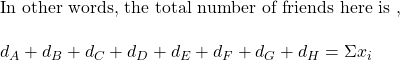
which we know is 20. The average number of friends is obtained by dividing this by the total number of individuals, n.
![]()
Now, we will move to the total friends of friends.

which was 60/20 in our case. If you are confused, remember these:
| the total number of individuals = n the avg. number of friends of individuals = total number of friends / total number of individuals the avg. number of friends of friends = total number of friends of friends / total number of friends |
Back to the equations.
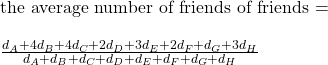
Look carefully, dA appears once in the numerator, and dA has one friend (B). dB appears four times and dB has four friends, and so on. This is no accident as the number of friends is counted multiple times as they appear in the friends’ friends list. Apply this rule to the equation, and you get.
![Rendered by QuickLaTeX.com \\ \text{the average number of friends of friends = } \\\\ \frac{d_A*d_A + d_B*d_B + d_C*d_C + d_D*d_D + d_E*d_E + d_F*d_F + d_G*d_G + d_H*d_H}{d_A + d_B + d_C + d_D + d_E + d_F + d_G + d_H} \\ \\ = \frac{d_A^2 + d_B^2 + d_C^2 + d_D^2 + d_E^2 + d_F^2 + d_G^2 + d_H^2}{d_A + d_B + d_C + d_D + d_E + d_F + d_G + d_H} \\ \\ = \frac{\Sigma{x_i^2}}{\Sigma{x_i}} \\ \\ \text{divide the numerator and the denominator by n} \\ \\ = \frac{\Sigma{x_i^2}/n}{\Sigma{x_i}/n} \\ \\ \text{add and subtract } (\Sigma{x_i})^2/n^2 \text { at the numerator} \\ \\ = \frac{[\Sigma{x_i^2}/n + (\Sigma{x_i})^2/n^2 - (\Sigma{x_i})^2/n^2]}{\Sigma{x_i}/n} \\ \\ = \frac{[\Sigma{x_i^2}/n - (\Sigma{x_i})^2/n^2]}{\Sigma{x_i}/n} + \frac{[(\Sigma{x_i})/n]^2}{\Sigma{x_i}/n} \\ \\ = \frac{[\Sigma{x_i^2}/n - (\Sigma{x_i})^2/n^2]}{\Sigma{x_i}/n} + {\Sigma{x_i}/n}](https://thoughtfulexaminations.com/wp-content/ql-cache/quicklatex.com-786ce585899542d9a42a1b8449675861_l3.png)
The second term, we know from the earlier section, is the average number of friends of individuals. The first term is nothing but the variance divided by the mean.
The mean number of friends of friends = (mean of friends ) + (variance / mean), which is equal to or greater than the mean of friends.
References
Why do your friends have more friends than you do? The American Journal of Sociology
The friendship paradox: MIT Blossoms

