We have seen the girl paradox in one of the older posts. Today we do a series of variations of the problem using Bayes’s equation. Sorry, Bayes-Price-Laplace equation! In a town far far away, every household has exactly two children.
The probability of two girls in a family
![]()
The probability of two girls in a family, if you know, they have at least one girl.
We use the generalised equation here.
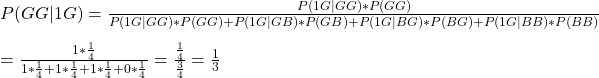
I guess you don’t need a lot of explanations. B represents a boy, and G represents a girl. The prior probability of each combination, BB, BG, GB or GG, is (1/4); equally likely.
The probability of two girls in a family, if you know, a family has a girl named Florida. Florida is a girl’s name, and let p is the probability of a girl named Florida.
![Rendered by QuickLaTeX.com \\ P(GG|F) = \frac{P(F|GG)*P(GG)}{P(F|GG)*P(GG) + P(F|GB)*P(GB) + P(F|BG)*P(BG) + P(F|BB)*P(BB)} \\\\ = \frac{[p(1-p)+(1-p)p+p^2]*\frac{1}{4}}{[p(1-p)+(1-p)p+p^2]*\frac{1}{4} + p*\frac{1}{4} + p*\frac{1}{4} + 0*\frac{1}{4}} = \frac{(2p-p^2)*\frac{1}{4}}{(2p-p^2)*\frac{1}{4} + p*\frac{1}{4}} = \frac{2-p}{4-p}](https://thoughtfulexaminations.com/wp-content/ql-cache/quicklatex.com-3523721d77ba64c93a37e31f950d8746_l3.png)
You may be wondering where that long-expression for P(F|GG) comes from. It’s the total probability of having a girl named Florida, regardless of whether they have already a daughter named Florida. So p(1-p) (the first girl is Florida and the other girl is not), (1-p)p (the second girl is Florida and the other girl is not), and p2 (both girls are Florida).
This is interesting. If the probability of a girl’s name Florida is 1, or every girl is named Florida, then P(GG|F) = (1/3) = P(GG|1G). If the name is rare or close to zero, P(GG|F) becomes (1/2).

