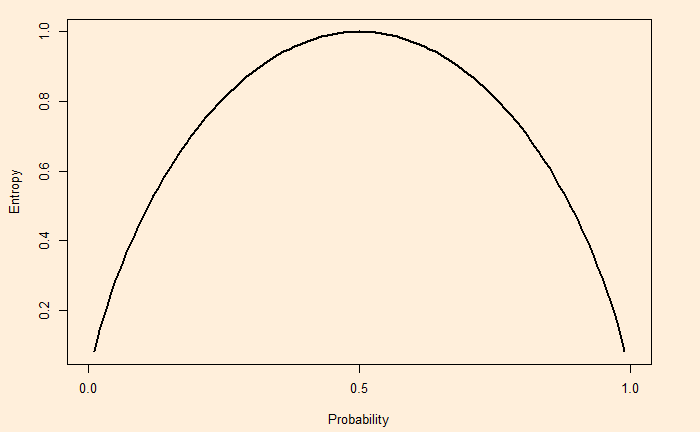
We have seen how the entropy of a system is derived as the surprise element of a system. The higher the entropy, the higher the surprise, ignorance or the degree of disorder of the system.
As an extreme example, the entropy of a double-headed coin is zero as it contains no information, i.e., always lands on heads!
![\\ H = \sum\limits_{x=0}^{n} p(x) log_2[\frac{1}{p(x)}] \\\\ = 1 * log_2[\frac{1}{1}] + 0 * log_2[\frac{1}{0}] = 0](https://thoughtfulexaminations.com/wp-content/ql-cache/quicklatex.com-71946fe8b18e9e4a7d355da917b21654_l3.png "Rendered by QuickLaTeX.com")
On the other hand, a fair coin (50-50) produces a non-zero entropy. The full spectrum of entropy for a coin toss is:
