Here we are, with another dice dual. I hope you recall the last banana problem. The setting is the same; there are two dice to roll, and the player who gets the higher number will win. But there is a problem the dice are not the normal ones like we know.
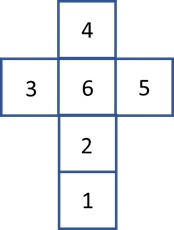
But they are of the four following ones.
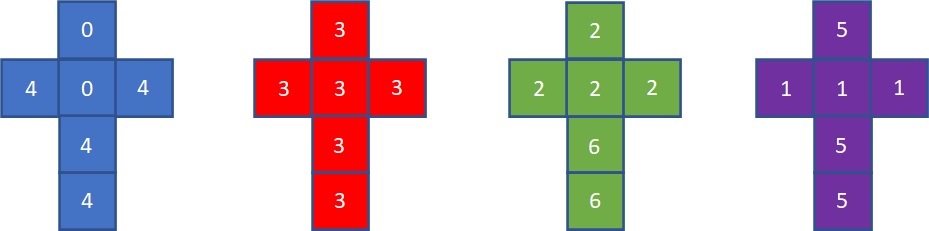
Angela and Ben are playing this game. Angela has the advantage of choosing the first die; Ben then picks from the remaining three. Which one should Angela pick? Can Angela win this game at all?
Angela thinks we can win this, for she has the first chance to choose. She compares purple and green. Let’s see what she gets. Here is the R code.
repeat_game <- 10000
win_perc_A <- replicate(repeat_game, {
die_cast1 <- sample(c(2,2,2,2,6,6), size = 1, replace = TRUE, prob = c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6))
die_cast2 <- sample(c(1,1,1,5,5,5), size = 1, replace = TRUE, prob = c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6))
if (die_cast1 > die_cast2) {
counter = 1
} else {
counter = 0
}
}
)
mean(win_perc_A)Well, the green wins two out of three. Here are all the possibilities in a tabular form.
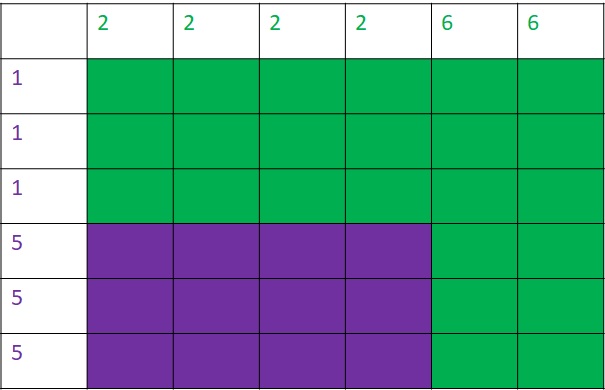
She then compares green and red, and the outcome favours red:.
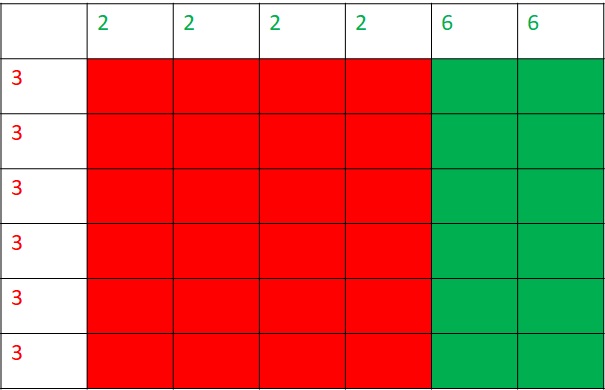
Finally, the blue and the red, and the former wins.
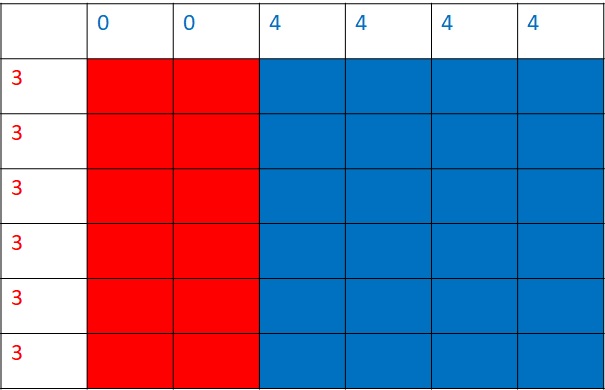
Since purple < green < red < blue, she thinks, blue is the winner die. And she picks it. When angela chose blue, Ben took the last one – purple. Look at the outcome.

Purple defeats blue!
Bradley Efron, professor of statistics and biomedical data science at Stanford University, is the man behind the invention of these dice. The interesting fact is that no matter which one the first person chooses, the second person always selects something better.

