Cournot Duopoly is an economic strategy game where two firms producing the same type of products compete for the market by controlling their output. It is a simultaneous move game, and there is no collusion.
Let the firms be 1 and 2 choosing to produce q1 and q1 quantity of goods. In this model, they only decide how much to make. The price will be determined by the market using an inverse demand curve. So, price P = a – b x Q, where Q = q1 + q2 and a and b are positive numbers.
The marginal costs of production are C1 and C2, respectively. These suggest the profit of firm 1, Profit 1 = revenue – cost = P x q1 – C1 x q1. Similarly, Profit 2 = P x q2 – C2 x q2.
Profit 1 = (a – b x (q1 + q2) )x q1 – C1 x q1
= (a – bq1 – bq2 – C1)q1
Profit 2 = (a – bq1 – bq2 – C2)q2
Nash Equilibirum
To get the Nash equilibrium, we’ll maximise the payoffs (profits) of firm 1 and firm 2 by differentiating with respect to q1 and q2 and setting them to zero.
d(Profit 1) / d(q1) = a – 2bq1 – bq2 – C1 = 0
d(Profit 2) / d(q2) = a – bq1 – 2bq2 – C2 = 0
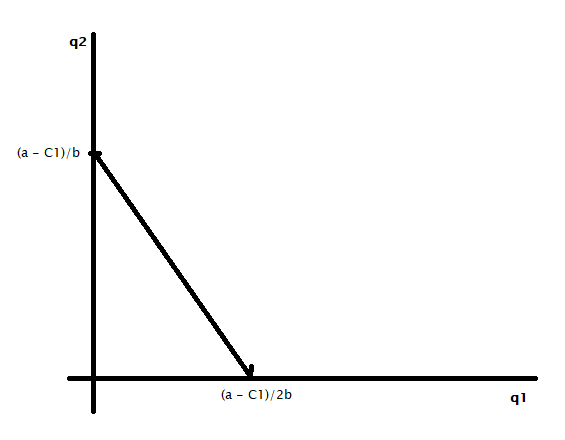
q1 = (a – bq2 – C1)/2b
q2 = (a – bq1 – C2) / 2b
So, q1 is a function of q2 and vice versa. The first equation, a straight line, will look like the following.