Consider a large population from which you are randomly sampling 1000 people. The ask is to get a simple YES or NO answer from each survey participant about a candidate. Suppose 450 people gave a YES answer; what is the margin of error in the estimate if you use a confidence level of 95%?
![]()
The sample size, n = 1000. Since 450 out of 1000 responded YES, we approximate the value 450/1000 (the sample ratio, h) as the population probability (p) for YES. The next step is to estimate sigma, the standard deviation. This can be done in two ways.
Solution as Bernoulli trial
This is a Bernoulli trial, and the standard deviation per trial is nothing but the square root of p x (1-p), where p is the probability of YES.
sd = root(p x (1-p) = root(0.45 x 0.55) = 0.497.
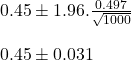
Thus, the population percentage p is in the interval [0.45 – 0.031, 0.45 + 0.031] or [0.42, 0.48] at 95% confidence interval.

